Загальні поняття

Лекція 13. Перевірка статистичних гіпотез

13.1. Загальні поняття.

13.2. Перевірка гіпотези щодо рівності дисперсій двох нормально

розподілених генеральних сукупностей.

13.3. Перевірка гіпотези щодо рівності двох середніх нормальних

генеральних сукупностей.

13.4. Перевірка гіпотези щодо рівності вибіркової середньої

математичному сподіванню.

13.5. Критерій згоди відносно частоти.

13.6. Критерії згоди щодо закону розподілу.

13.7. Питання для самоперевірки.

Будь-яке судження про генеральну сукупність за результатами дослідження вибіркової сукупності є гіпотезою. Статистичною гіпотезою є припущення відносно параметрів або закону розподілу випадкової величини. Вихідне твердження про відсутність істотної відмінності між емпіричною та теоретичною характеристиками називається основною, або нульовою гіпотезою (). Саме вона і підлягає перевірці. У відповідності з нульовою гіпотезою значення параметру 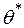, яке ми отримуємо за результатами дослідження вибіркової сукупності, дорівнює значенню цього параметру 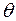у генеральній сукупності, тобто: 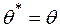. Протилежна гіпотеза, що розглядає наявність відмінності будь-якого знаку, називається конкуруючою, або альтернативною (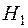). Альтернативна гіпотеза може мати різний зміст в залежності від задачі, що розглядається. Наприклад, або та інші.

Розрізняють гіпотези, які містять одне або більше одного припущень. Гіпотеза називається простою, якщо вона містить тільки одне припущення, якщо більше – то складною.

Наслідком перевірки гіпотези можуть бути правильні висновки двох типів: основну гіпотезу нема підстав відхилити, і ця гіпотеза дійсно є правильною, або основна гіпотеза відхиляється, і вона дійсно хибна.

Однак при перевірці статистичної гіпотези можна припуститись помилки. Ці помилки теж бувають двох типів. Помилка першого роду полягає в тому, що правильна нульова гіпотеза помилково буде відхилена («хибна тривога»). Ймовірність помилки першого роду називають рівнем значущості і позначають через 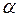. При статистичних дослідженнях зазвичай прийняті рівні значущості 0,05 та 0,01. Помилка другого роду полягає в тому, що хибна нульова гіпотеза буде прийнята («небезпека вчасно не буде поміченою»). Ймовірність помилки другого роду позначають через 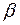. Оскільки помилки другого роду мають більш важкі наслідки, то в тому разі, коли виникають сумління, краще відхилити правильну нульову гіпотезу, ніж прийняти хибну.

Перевірка статистичної гіпотези здійснюється за допомогою статистичного критерію. Статистичним критерієм називають випадкову величину, яка застосовується для перевірки статистичної гіпотези. Позначення статистичного критерію може бути різним, це залежить від того, який саме критерій використовується. Побудова статистичного критерію передбачає вибір певної функції від результатів спостережень (емпіричних значень ознаки), яка використовується для визначення міри відмінності між емпіричними значеннями та гіпотетичними.

Статистичні критерії поділяються на параметричні і непараметричні. Параметричними є критерії, застосування яких передбачає обчислення параметрів розподілу ймовірностей ознаки (середнього та дисперсії). До цієї групи належать критерій Стьюдента (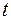– критерій), критерій Пірсона (критерій 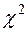), критерій Фішера (– критерій). При користуванні непараметричними критеріями застосовуються частоти або ранги. До цієї групи належать критерій Колмогоров, критерій Вілкоксона тощо.

Область припустимих значень відповідає значенням статистичного критерію, при яких нульову гіпотезу приймають. Слід зазначити, що нульову гіпотезу підтвердити неможливо, однак результати застосування статистичного критерію можуть свідчити про те, що вона не містить протиріч, отже, нема причин її відхилити. Критична область – це множина значень статистичного критерію, при яких нульова гіпотеза відхиляється на користь альтернативної. Критична область може бути двосторонньою або односторонньою. Критичними точками 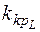та називають точки, що відділяють критичну область від області припустимих значень. Рівень значущості статистичного критерію дорівнює ймовірності події, яка полягає у тому, що при правильній нульовій гіпотезі значення статистичного критерію належатиме критичній області (ця область на рис. 13.1 заштрихована), що призведе до необхідності відхилити правильну нульову гіпотезу.

Рис. 13.1. Критична область статистичного критерію

Природно прагнути мінімізувати ймовірність статистичних помилок. Однак при зниженні рівня значущості 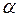, що супроводжується зменшенням ймовірності виникнення помилки I-го роду, збільшується ймовірність помилки II-го роду. Тому вводять поняття потужності критерію. Величина 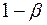називається потужністю критерію і визначає ймовірність попадання значення статистичного критерію до критичної області за умови, що альтернативна гіпотеза є справедливою. Одночасно зменшити ймовірність похибок І-го та ІІ-го родів можна тільки завдяки збільшенню обсягу вибіркової сукупності.

Усі статистичні критерії припускають деякий конкретний тип математичної моделі (наприклад, нормально розподілена сукупність із заданим значенням дисперсії). На практиці умови, які ставить математична модель, можуть і не виконуватися, що призводить до зростання ймовірності неправильних висновків, які роблять на основі критерію, що розглядається. Для одних критеріїв подібне зниження надійності висновків відбувається у більшій мірі, ніж для інших. Стійкими,або робастними, називають критерії, для яких помірні відхилення сукупності від математичної моделі, що припускається, мало впливають на надійність висновків.

Типовий алгоритм перевірки статистичних гіпотез передбачає:

1. Формулювання нульової та альтернативної 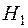гіпотез.

2. Вибір критеріальної статистики (статистичного критерію).

3. Вибір рівня значущості .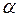

4. Обчислення емпіричного значення статистичного критерію.

5. Порівняння емпіричного і критичного значень критерію.

6. Висновки щодо статистичної значущості розбіжностей значень числових характеристик, що розглядаються нульовою гіпотезою.

Для перевірки гіпотез використовуються різні статистичні критерії залежно від задачі, що розглядається.

Дата добавления: 2014-01-04