Вибіркової середньою математичному сподіванню

Перевірка гіпотези щодо рівності

Припустимо, що треба перевірити основну гіпотезу щодо рівності генеральної середньої, статистичною оцінкою якої є вибіркова середня, і математичного сподівання випадкової величини, тобто 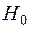: 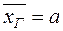. В якості статистичного критерію вибираємо випадкову величину

,

де 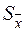– стандартна похибка вибіркової середньої:

.

Отже, статистичний критерій має вигляд:

, (13.5)

де 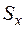– виправлене середнє квадратичне відхилення випадкової величини .

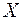Випадкова величина 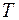має розподіл Стьюдента з кількістю степенів свободи . Якщо 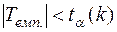, то нульову гіпотезу нема підстав відхилити. Якщо 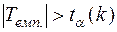, то з надійністю 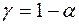нульова гіпотеза відхиляється на користь альтернативної.

Критична область статистичного критерію залежить від вигляду альтернативної гіпотези. Якщо альтернативна гіпотеза полягає у тому, що 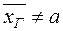, то критична область є двосторонньою. У цьому разі поняття припустимого інтервалу для статистичного критерію збігається з поняттям довірчого інтервалу для математичного сподівання (12.6), а саме:

.

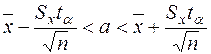Приклад. З партії товару вибрано 16 одиниць для вибіркового контролю щодо відповідності нормі всієї партії товару. За результатами вимірювання виявилось, що 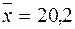та 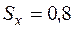. Перевірити з надійністю 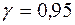, чи можна вважати відмінності між генеральною середньою та математичним сподіванням, яке повинно дорівнювати 20, статистично незначущими.

Розв’язання. Перевірці підлягає основна гіпотеза 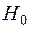: 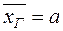при альтернативній 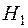: 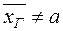, отже, критична область є двосторонньою. Перевірку здійснюємо за критерієм Стьюдента. Визначаємо емпіричне значення критерію: 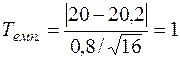. За умовою прикладу маємо, що 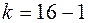, , 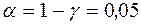отже, за таблицею значень для статистики Стьюдента визначаємо 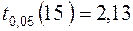. Оскільки 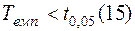, то нульову гіпотезу нема підстав відхилити, тобто за результатами вибіркового контролю можна вважати, що властивості партії товару відповідають нормі.

Дата добавления: 2014-01-04