Однофакторний дисперсійний аналіз

Основні положення дисперсійного аналізу

Лекція 14. Елементи дисперсійного аналізу

14.1. Основні положення дисперсійного аналізу.

14.2. Однофакторний дисперсійний аналіз.

14.3. Поняття про двофакторний дисперсійний аналіз.

14.4. Питання для самоперевірки.

Дисперсійний аналіз є методом багатовимірної статистики, який дозволяє здійснювати дослідження впливу якісних факторів і аналізу значущості цього впливу. При дослідженні економічних процесів та явищ дисперсійний аналіз може використовуватися для виявлення спільного впливу економічних факторів, що не піддаються кількісному виміру, на економічний показник, що досліджується.

Суть методу полягає в тому, що загальна варіація (мінливість) показника – результату − розподіляється на частини, що відповідають роздільному або спільному впливу різних якісних факторів, і залишкову варіацію, що акумулює вплив тих факторів, які не враховує дана модель. Отже, загальна дисперсія фактора, що характеризує певний процес, тобто внутрішнього фактора системи, є сумою двох компонентів: дисперсії, яка обумовлена впливом зовнішніх контрольованих факторів, і дисперсії, що пов’язана з похибками моделі, тобто обумовлена впливом факторів, які не розглядаються в межах даної моделі. Статистичне вивчення цих частин дозволяє робити висновки про те, чи дійсно впливає на результат той або інший якісний фактор. При цьому вважається, що досліджувана ознака має нормальний закон розподілу, а дисперсії в кожній окремій групі здобутих значень ознаки однакові (ці припущення необхідно перевіряти перед тим, як застосовувати дисперсійний аналіз).

Дисперсійний аналіз дозволяє оцінити наявність стохастичного зв’язку у системі одновимірних випадкових величин, не висловлюючи при цьому ніяких припущень відносно природи цього зв’язку. Наприклад, в якості фактора впливу може розглядатися організація виробництва на різних виробничих ділянках, які оснащені приблизно однаковим устаткуванням. Тоді розходження у кількості (або якості) продукції, що випускається цими ділянками у розрахунку на одного працюючого, визначаються розходженнями в способах організації виробництва на різних ділянках.

Дисперсійний аналіз, який досліджує наявність стохастичного зв’язку між компонентами двовимірної випадкової величини, називається однофакторним. При проведенні однофакторного дисперсійного аналізу масив емпіричних даних – це значення одного з компонентів двовимірної випадкової величини, який називається ознакою, – поділяють на групи за рівнем фактора, що впливає на ознаку – це інший компонент двовимірної випадкової величини.

Результати експерименту зручно представляти у вигляді спеціальної таблиці (табл. 14.1).

Таблиця 14.1

Таблиця вихідних даних дисперсійного аналізу

Рівень фактора (номер групи)	Емпіричні значення якісної ознаки за групами	Середня випадкової величини	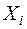Загальна (вибіркова) середня ознаки
			,
...	............................	............................

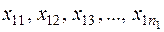
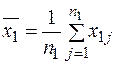
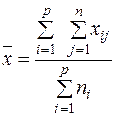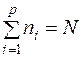
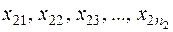
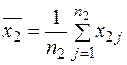
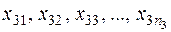
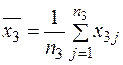
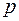
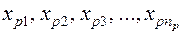
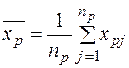
Відповідно до моделі однофакторного дисперсійного аналізу цим даним можна надати наступну інтерпретацію. Нехай є випадкові величини 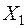, ,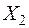..., , 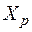що розподілені за нормальним законом і мають однакові, хоча й невідомі, дисперсії. Математичні сподівання цих величин невідомі, вони можуть бути як рівними, так і різними.

Для кожної з величин 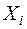(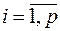) проведено відповідно 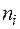вимірювань, результати яких надані в табл. 14.1. Необхідно при заданому рівні значущості 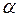перевірити статистичну гіпотезу 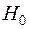, яка в даному випадку полягає в тому, що різниця між математичними сподіваннями всіх випадкових величин є статистично незначущою. Перевірка гіпотези здійснюється за критерієм Фішера – Снедекора.

Згідно із положеннями дисперсійного аналізу загальну суму квадратів відхилень значень випадкової величини від її вибіркової середньої, що характеризує загальне розпорошення випадкової величини, надають у вигляді суми двох компонентів:

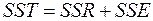(14.1)

де 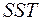− загальна сума квадратів відхилень значень випадкової величини від її вибіркової середньої (sum of squares total);

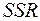− сума квадратів відхилень, що пов’язані з регресією, тобто з впливом досліджуваного фактора (sum of squares by regression);

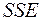− сума квадратів помилок, тобто відхилень, що пов’язані з факторами, які не розглядаються в межах даної моделі, і вважаються похибками (sum of squares by errors).

Поряд з термінами 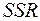та 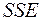, які є загальноприйнятими в сучасних підручниках, де розглядаються питання багатовимірної статистики, та в пакетах прикладних програм, у класичних підручниках з теорії ймовірностей та математичної статистики зустрічаються близькі за змістом до вище згадуваних терміни факторна (це інша назва 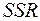) і залишкова (це інша назва 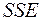) суми квадратів відхилень, а також міжгрупова та внутрішньогрупова дисперсії, які визначаються як питомі суми квадратів відхилень 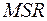і 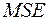, тобто відношення відповідних сум до кількості ступенів вільності (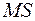− середні квадрати, або mean of squares). За означенням поділ загальної дисперсії на складові здійснюється таким чином:

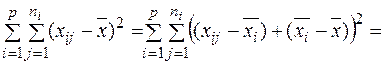
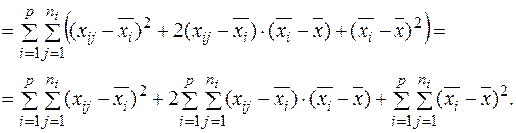
Враховуючи те, що вибіркова середня має наступну властивість:

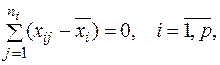
то як наслідок перетворення другого члена попереднього співвідношення отримуємо, що

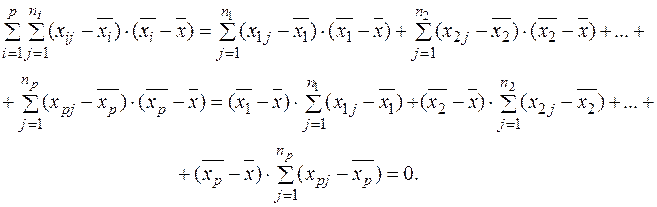
Тепер для третього члена суми отримуємо:

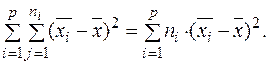
Таким чином, отримуємо:

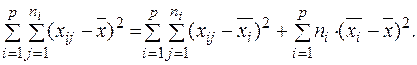(14.1^І)

Із порівняння співвідношень (14.1) і (14.1^І) визначимо сенс кожного доданка загальної суми квадратів відхилень. Так, загальна сума квадратів відхилень значень випадкової величини від її вибіркової середньої визначається за формулою:

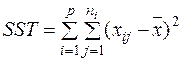, (14.2)

де 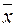− загальна (вибіркова) середня, тобто середня вибіркової сукупності випадкових величин 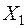, ,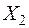..., 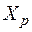обсягом .

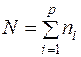Сума квадратів відхилень, що пов’язані з регресією, тобто розпорошення під впливом певного зовнішнього фактора, визначається як виважена сума квадратів відхилень вибіркової середньої кожної з випадкових величин 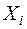(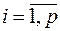) від загальної середньої ознаки . Оскільки обсяг кожної групи може бути різним, то ваговий коефіцієнт дорівнює обсягу відповідної вибіркової сукупності 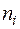за певною групою ().

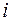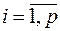Таким чином для визначення 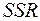маємо формулу:

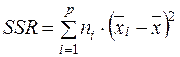, (14.3)

де 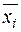− вибіркова середня випадкової величини ().

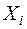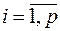Сума квадратів відхилень певної випадкової величини 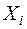(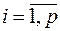) від її вибіркової середньої (тобто розпорошення випадкової величини 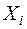у межах кожної вибіркової сукупності обсягом 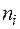) вважається розпорошенням, що пов’язане з похибками. Насправді це можуть бути не тільки похибки вимірювання, але і помилки (неправильне припущення) самої моделі, тобто це розпорошення може бути пов’язаним з факторами, що не враховані в межах даної моделі. Сума квадратів помилок визначається за формулою:

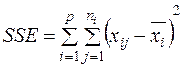. (14.4)

Для перевірки статистичної гіпотези щодо однорідності всієї вибіркової сукупності в цілому, тобто для перевірки гіпотези 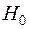, розглядають випадкову величину 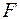, що розподілена за статистикою Фішера. Вона визначається як відношення питомої суми квадратів відхилень ознаки від її вибіркової середньої (тобто суми квадратів відхилень, що припадає на одну ступінь вільності) під дією фактора, вплив якого розглядається в даній моделі, до питомої суми квадратів відхилень, котрі обумовлені чинниками, які не враховуються в межах даної моделі. Отже, емпіричне значення критерію Фішера – Снедекора визначається за формулою:

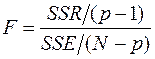, (14.5)

де 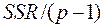− питома сума квадратів відхилень, що пов’язані з впливом досліджуваного фактора;

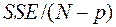− питома сума квадратів відхилень, що пов’язані з випадковими причинами (помилки моделі).

Оскільки спостереження, за якими робиться висновок щодо відсутності впливу певного якісного фактора на ознаку, за рівнем значення фактора об’єднані в 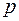груп, тобто маємо 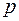об’єктів, за якими зроблено висновки, то кількість ступенів свободи при визначенні 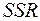дорівнює .

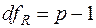Відносно ступенів вільності дисперсій виконується співвідношення:

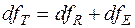. (14.6)

Оскільки загальна кількість ступенів свободи за вибірковою сукупністю обсягом 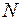становить 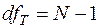, то для 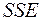кількість ступенів свободи, яка визначається як різниця між цими значеннями для вибірки в цілому і для дисперсії, що обумовлена впливом зовнішнього фактора, становить 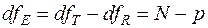. Отже, як чисельник, так і знаменник у формулі (14.5) мають сенс статистичних оцінок дисперсій, що пов’язані з різними джерелами варіації ознаки.

За основною гіпотезою 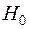, яка саме і підлягає перевірці, вважається, що для всіх рівнів значення якісного фактора, для котрих здійснюється дослідження, математичне сподівання ознаки є сталою величиною, тобто: 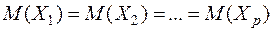. Це передбачає, що дисперсія ознаки внаслідок зміни значення фактора, вплив якого досліджується, не перевищує дисперсії ознаки, що пов’язана з випадковими помилками. За альтернативною гіпотезою 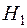дисперсія ознаки під впливом фактора, що досліджується, суттєво перевищує дисперсію ознаки, яка обумовлена впливом випадкових помилок.

Випадкова величина 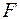(14.5) розподілена за статистикою Фішера –Снедекора із степенями свободи 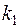(кількість степенів свободи чисельника − більшої з дисперсій) та 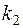(кількість степенів свободи знаменника − меншої з дисперсій). Постановка задачі має сенс, якщо більшою з дисперсій є дисперсія ознаки під впливом фактора, що досліджується. Отже, 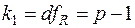, тоді як .

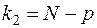У протилежному випадку, тобто коли оцінка вибіркової дисперсії всередині груп перевищує оцінку дисперсії між групами, можна без визначення критерію Фішера − Снедекора зробити висновок про статистичну незначущість відмінностей між середніми випадкових величин у групах, які відповідають різним рівням зовнішнього фактора.

Відповідно до прийнятого заздалегідь рівня значущості 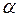та за кількістю степенів свободи обох дисперсій знаходимо критичну точку розподілу Фішера − Снедекора .

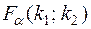Результати дисперсійного аналізу можна представити у вигляді таблиці (табл. 14.2).

Таблиця 14.2

Дата добавления: 2014-01-04