Теорема 2. Від будь-якої точки можна відкласти вектор, що дорівнює даному

Сумою двох векторів і називається вектор (правило трикутника; рис. 2). Вектори можна також додавати за правилом паралелограма: сумою векторів і є вектор —діагональ паралелограма ABCD.

Рис. 2

Зауваження. Оскільки від будь-якої точки площини можна відкласти вектор, що дорівнює даному, то для того, щоб додати два довільно розміщені вектори, достатньо від кінця одного з них відкласти вектор, що дорівнює другому, і скористатися правилом трикутника.

Вектор-називається протилежним вектору . Різницею векторів і 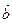називається сума вектора і вектора, протилежного вектору 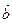, тобто 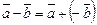(див. рис. 2).

Теорема 3 (про єдиність розкладу вектора на площині). Нехай на площині дано два неколінеарних вектори і . Тоді будь-який третій вектор у цій площині можна в єдиний спосіб подати у вигляді суми:

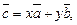
де х і у — числа, що називаються коефіцієнтами розкладу вектора за векторами і .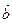

Лема. Якщо в Δ АВС точка D лежить на стороні АС і 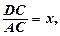то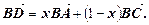

Задача. Нехай у Δ АВС точка N лежить на стороні ВС, а точка М — на стороні АВ, причому BN: ВР =1: 5; AM: АВ = 1: 5. Прямі AN і CM перетинаються в точці О. Знайти відношення СО: МС і АО: AN (рис. 3).

Рис. 3

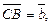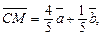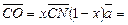
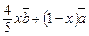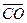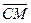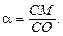Ø Введемо вектори тоді (за лемою). Позначимо Тоді з Δ ACN за лемою дістанемо: . Оскільки век­тори і колінеарні, то де Тому .

Беручи до уваги єдиність розкладу вектора за неколінеарними векторами і 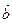, маємо систему рівнянь:

Розв’язавши її, дістанемо відповідь: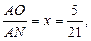

16.2. Скалярний добуток векторів,
його властивості

Кутом між векторами називається кут між променями, на яких лежать ці вектори.

Скалярним добутком векторів і (позначають або 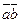) називається число, що дорівнює добутку довжин цих векторів, помноженому на косинус кута між ними:

(α — кут між векторами і ).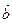

Зауваження. Якщо вектори і 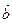взаємно перпендикулярні, то .

Виконуються такі властивості скалярного добутку:

l) ;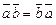

2) ;

3) .

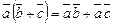З означення скалярного добутку випливає:

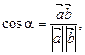
Векторний метод ефективно використовується при розв’язуванні геометричних задач.

Задача. У прямокутному трикутнику АВС 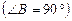AD — бісектриса ВМ — медіана трикутника (рис. 4). Знайти кут між AD і ВМ, якщо АВ = 3, ВР = 4.

Рис. 4

Ø За теоремою Піфагора дістаємо Згідно з теоремою теоремі про бісектрису внутрішнього кута 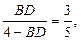звідки . Позначимо , Тоді , , 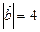. Оскільки 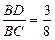, то , ; .

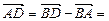
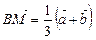Знайдемо довжину вектора : .

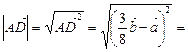
Враховуючи, те, що медіана прямокутного трикутника, проведена до гіпотенузи, дорівнює половині гіпотенузи, дістаємо

Обчислюємо скалярний добуток:

Отже,

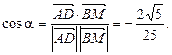
Задача. Знайти кут між діагоналлю АС ₁ і ребром AA ₁ паралелепіпеда ABCDA ₁ B ₁ C ₁ D ₁ (рис. 5), коли відомо, що AA ₁ = AD = 2, АВ = 1, .

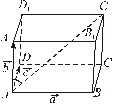
Рис. 5

Ø Введемо три вектори: , ,

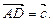
При цьому маємо: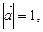

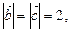
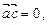
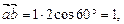
Вектор 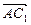подається через вектори 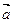, 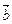і дуже просто:

Тому

.

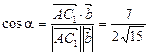16.3. Координати вектора

Якщо на площині задано два взаємно перпендикулярні (базис­ні) вектори і , такі що 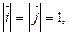то будь-який вектор 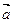площини можна в єдиний спосіб подати у вигляді:

.

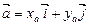Величини х_а і у_а називаються координатами вектора 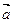. Позначають: .

Аналогічно, якщо у просторі задано три взаємно перпендикулярні вектори , і 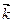, то будь-який вектор 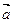простору можна в єдиний спосіб подати у вигляді

де x_a, y_a, z_a — координати вектора 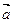. Позначення: .

Дата добавления: 2014-01-04