Властивості координат вектора

1. Рівні вектори мають рівні координати, тобто якщо , то x_a = x_b, y_a = y_b, z_a = z_b.

2. При множенні вектора на число його координати множать на те саме число, тобто якщо то x_a = λ x_b, y_a = λ y_b, z_a = λ z_b.

3. При додаванні векторів їхні координати додають, тобто якщо 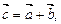то x_c = x_a + x_b, y_c = y_a + y_b, z_c = z_a + z_b.

4. Скалярний добуток двох векторів дорівнює сумі добутків відповідних координат цих векторів:

. (1)

5. Модуль вектора дорівнює кореню квадратному із суми квад­ратів його координат:

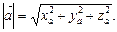(2)

Якщо у просторі дві точки А (х ₀, y ₀, z ₀) задано їхніми координатами і В (х ₁, y ₁, z ₁), то вектор має координати, що дорівнюють різниці відповідних координат початку і кінця вектора, тобто

Задача. Знайти координати точки D і кут між діагоналями паралелограма ABCD, якщо А (0, 1, – 2), В (– 1, 0, 3), С (2, 3, – 1).

Ø Нехай точка D має координати (х, у, z). Знайдемо координати векторів і :

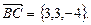
Оскільки ABCD — паралелограм, то Звідси випливає, що х = 3, у – 1 = 3, z + 2 = – 4, тобто х = 3, у = 4, z = – 6. Знайдемо тепер координати діагоналей:

Використовуючи формулу (2) для довжини вектора і формулу (1) для скалярного добутку векторів через його координати, ді-
стаємо:

16.4. Векторний добуток

Векторним добутком двох векторів 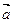і 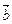називається вектор що задовольняє такі умови:

1)

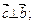
2) , α — кут між 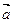і ;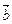

3) трійка 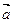, 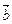і має праву орієнтацію, тобто з кінця вектора поворот від вектора 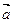до вектора 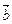на найменший кут бачимо проти годинникової стрілки (рис. 1).

Рис. 1

Дата добавления: 2014-01-04