
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основні теоретичні положення
|
|
|
|
Лекція №15-16. Комплексні числа.
Опорні конспекти лекцій
І КУРС
Лисенко В.І.
«Вища математика»
Література:
1. Гусак А.А. Высшая математика: учебник для студентов вузов. В 2 т. Т.1. – Минск: ТетраСистемс, 2007 – 544с. (76-91 с.).
2. Кривуца В.Г., Барковський В.В., Барковська Н.В. Вища математика. Практикум: Навчальний посібник: К.: Центр навч. літератури, 2005 – 536с. (с. 23-34).
Необхідність добування кореня парного степеня з дійсних від’ємних чисел привела до поняття комплексних чисел, які широко використовуються в сучасній математиці та її застосуваннях.
1. Поняття комплексного числа. Форми його запису.
Озн.1. Комплексним числом називають вираз виду 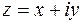 , де
, де  та
та  – дійсні числа,
– дійсні числа,  – уявна одиниця.
– уявна одиниця.
Число  – називають дійсною частиною комплексного числа
– називають дійсною частиною комплексного числа  і позначають
і позначають  (від латинського realis (дійсний)); число
(від латинського realis (дійсний)); число  , що є коефіцієнтом при уявній одиниці
, що є коефіцієнтом при уявній одиниці  , називають уявною частиною комплексного числа
, називають уявною частиною комплексного числа  і позначають
і позначають  (від латинського imaginarins (уявний)).
(від латинського imaginarins (уявний)).
Якщо 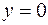 , то
, то  , тобто
, тобто  співпадає з дійсним числом
співпадає з дійсним числом  .
.
Якщо  , то
, то  – суто уявне число.
– суто уявне число.
Комплексні числа  та
та  рівні, якщо рівні їх дійсні та уявні частини. Тобто
рівні, якщо рівні їх дійсні та уявні частини. Тобто 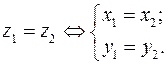
Комплексне число 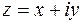 у декартовій системі координат можна зобразити точкою з координатами
у декартовій системі координат можна зобразити точкою з координатами 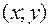 . При цьому між точками площини і комплексними числами встановлюється взаємооднозначна відповідність. Дійсна частина
. При цьому між точками площини і комплексними числами встановлюється взаємооднозначна відповідність. Дійсна частина  зображується точками осі Ох, яку називають дійсною віссю. Уявна частина
зображується точками осі Ох, яку називають дійсною віссю. Уявна частина  –зображується точками осі Оу, яку називають уявною віссю.
–зображується точками осі Оу, яку називають уявною віссю.
Кожній точці площини Оху відповідає її радіус-вектор  (вектор, що з’єднує початок координат з точкою) і полярний кут
(вектор, що з’єднує початок координат з точкою) і полярний кут 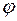 (кут повороту осі Ох до радіус-вектора
(кут повороту осі Ох до радіус-вектора  ),
),
Числа 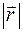 і
і 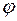 називають модулем та аргументом комплексного числа і позначають
називають модулем та аргументом комплексного числа і позначають 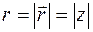 ,
, 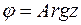 .
.
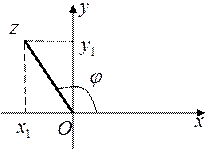 |
Рис.1
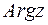 визначається з точністю до
визначається з точністю до  , його головне значення
, його головне значення  .
.
Комплексне число  можна записувати в трьох формах:
можна записувати в трьох формах:
алгебраїчна  (1)
(1)
тригонометрична  (2)
(2)
показникова  (3)
(3)
Для переходу від алгебраїчної форми запису комплексного числа  до тригонометричної або показникової форм використовують формули:
до тригонометричної або показникової форм використовують формули:
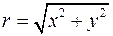 ,
,  ,
, 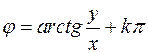 (4)
(4)
 |
Рис.2
Озн.2. Комплексне число 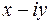 називають комплексно спряженим до числа
називають комплексно спряженим до числа 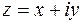 і позначають
і позначають  (читають z з рискою).
(читають z з рискою).
Примітка 1: Щоб визначити чверть, якій належить 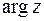 , слід керуватись такими міркуваннями:
, слід керуватись такими міркуваннями:
| Чверть | Межі зміни 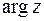
| Знаки | |
| х | у | ||
| І | 
| + | + |
| ІІ | 
| – | + |
| ІІІ | 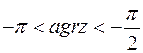
| – | – |
| ІV | 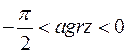
| + | – |
Приклад 1. Знайти модулі та головні значення аргументів чисел:
а) 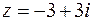 , б)
, б)  , в)
, в)  .
.
Розв’язання:
а) 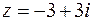 ,
,
(4):  ,
,  (ІІ чверть)
(ІІ чверть)  .
.

 ;
; 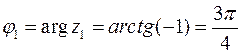 .
.
б)  ,
,
(4): 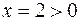 ,
,  (ІV чверть)
(ІV чверть)  .
.

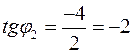 ;
;  .
.
в)  ,
,
(4):  ,
, 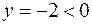
 – розміщено на осі Оу.
– розміщено на осі Оу.
 ;
;
 ; (
; ( не існує)
не існує)  .
.
Приклад 2. Записати дане комплексне число в іншій формі.
№

| Форма запису комплексного числа | ||
| Алгебраїчна | Тригонометрична | Показникова | |
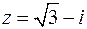
| |||

| |||
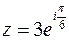
|
Розв’язання
1) 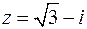 ,
,  ,
, 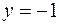 ;
;  – належить IV чверті.
– належить IV чверті.
(4):  ;
;  ;
; 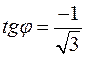 ;
;
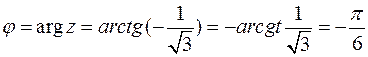 .
.
(2):  – тригонометрична форма запису.
– тригонометрична форма запису.
(3):  – показникова форма запису.
– показникова форма запису.
2)  .
.  – І чверть.
– І чверть.
(2)  ;
; 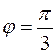 .
.
(4)  ,
,  ;
; 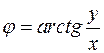 .
.

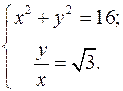
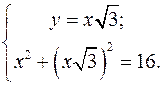

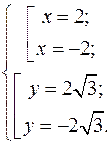


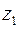 – належить І чверті, а
– належить І чверті, а 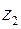 – ІІІ чверті.
– ІІІ чверті.
Відповідь: 
3) 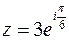 (3)
(3)  ;
;  ;
;  – І чверть.
– І чверть.
 – тригонометрична форма запису.
– тригонометрична форма запису.
(4) 
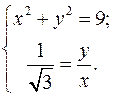

Оскільки 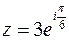 належить І чверті, то належить І чверті, то 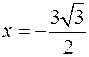 , , 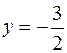 – сторонній розв’язок.
Відповідь: – сторонній розв’язок.
Відповідь:  – алгебраїчна форма запису. – алгебраїчна форма запису.
|
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 601; Нарушение авторских прав?; Мы поможем в написании вашей работы!