
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дії над комплексними числами
|
|
|
|
а) Дії над комплексними числами, заданими в алгебраїчній формі.
Оскільки кожному комплексному числу 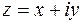 можна поставити у відповідність радіус-вектор точки
можна поставити у відповідність радіус-вектор точки 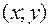 , то множення комплексного числа на дійсне число с та додавання (віднімання) комплексних чисел здійснюється аналогічно множенню на число та додаванню (відніманню) векторів, заданих своїми координатами.
, то множення комплексного числа на дійсне число с та додавання (віднімання) комплексних чисел здійснюється аналогічно множенню на число та додаванню (відніманню) векторів, заданих своїми координатами.
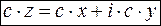 (5),
(5), 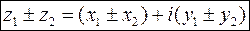 (6)
(6)
Приклад 3. Знайти 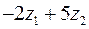 , якщо
, якщо 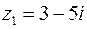 ,
, 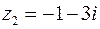 . Зобразити на рисунку:
. Зобразити на рисунку: 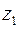 ,
, 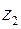 та
та 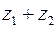 .
.
Розв’язання:
(5):  ,
, 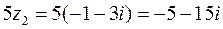 ,
,
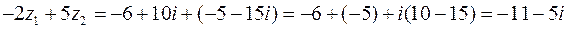 .
.
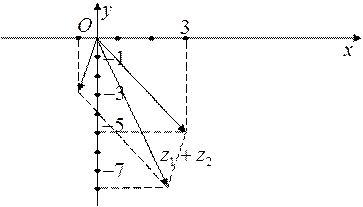 |
Рис.3
Множення комплексних чисел, заданих в алгебраїчній формі здійснюється за правилом множення многочленів та заміни 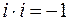 .
.
Для ділення комплексних чисел треба помножити ділене і дільник на число, яке комплексно спряжене до дільника, виконати вказані дії, щоб відокремити дійсну та уявну частини.
Приклад 4. Знайти 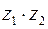 та
та 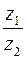 , якщо
, якщо 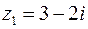 ,
, 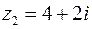 .
.
Розв’язання.
 ;
;
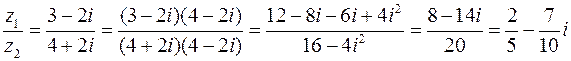 .
.
Примітка 2:
1. 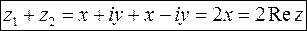 . (7)
. (7)
2. 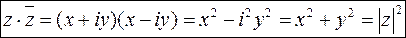 (8)
(8)
3. 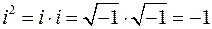 ;
; 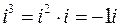 ;
; 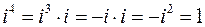 ;
;
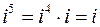 . Тобто
. Тобто 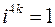 ,
, 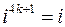 ,
,  ,
, 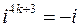 ,
,  .
.
б) Множення та ділення комплексних чисел, заданих у тригонометричній та показниковій формах.
При множенні комплексних чисел, заданих у тригонометричній або показниковій формах, їх модулі перемножають, а аргументи додають.
Якщо 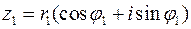 ,
, 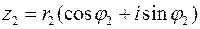 , то
, то
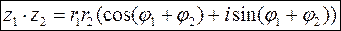 (9)
(9)
Якщо 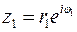 ,
,  , то
, то 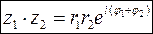 (
(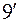 )
)
При діленні комплексних чисел, які задані в тригонометричній або в показниковій формах, їх модулі ділять, а аргументи віднімають.
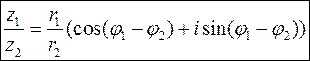 (10)
(10)
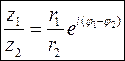 (
(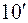 )
)
Приклад 5. Знайти: а) 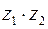 та
та 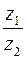 ; б)
; б)  та
та  , якщо
, якщо 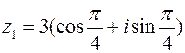 ,
,  ,
, 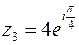 ,
,  .
.
Розв’язання:
а) 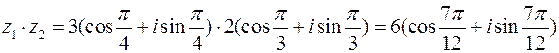 .
.
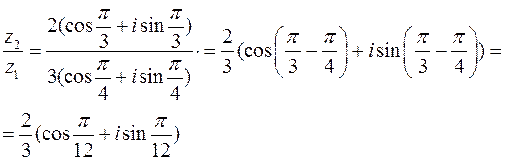
б) 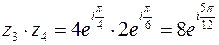 ,
, 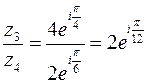 .
.
в) Піднесення до степеня та добування кореня з комплексного числа.
Піднесення до степеня і добування кореня доцільно виконувати, використовуючи тригонометричну або показникову форми запису комплексних чисел.
Правило множення комплексних чисел розповсюджується на будь-яку кількість множників, тому:
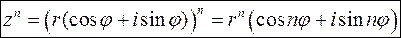 (11)
(11)
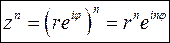 (
(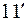 ).
).
Якщо 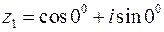 ,
, 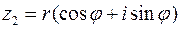 , то
, то
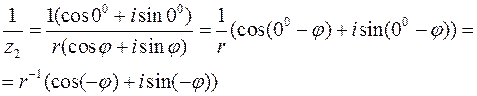
Тобто 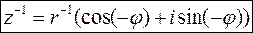 (
( )
)
Формулу (11) називають формулою Муавра.
Для знаходження n різних значень 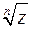 використовують формули:
використовують формули:
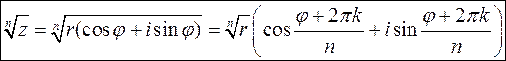 (12)
(12)
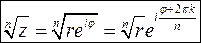 (
( ) де
) де 
Приклад 6. Знайти: а) 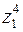 та
та 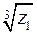 ; б)
; б) 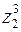 та
та 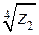 , якщо
, якщо 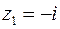 ,
, 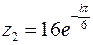 .
.
Розв’язання:
а) Запишемо число 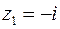 в тригонометричній формі:
в тригонометричній формі:

(11): 
Цей же результат одержимо 
(12): 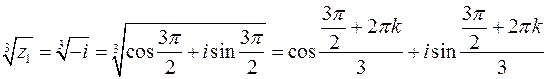 ,
,
де 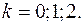
Одержимо при 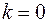 ,
, 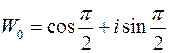 ;
;
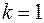 ,
, 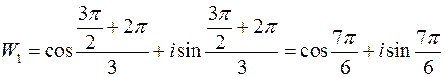 ;
;
 ,
, 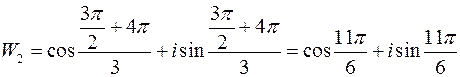 ;
;
б) 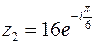 ;
;
(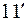 ):
):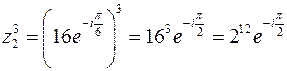 ,
,
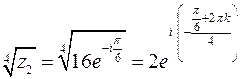 де
де 
Одержимо: при 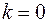 ,
, 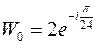 ;
;
при 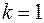 ,
, 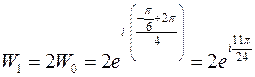 ;
;
при  ,
, 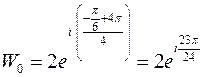 ;
;
при 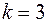 ,
, 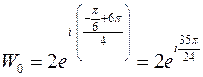 .
.
Питання для самоконтролю
1. Дайте означення комплексного числа; що таке дійсна та уявна частина комплексного числа?
2. Як визначається уявна одиниця?
3. Які комплексні числа називаються рівними; спряженими?
4. Як зображується комплексне число на площині?
5. Яка форма запису комплексного числа називається алгебраїчною; тригонометричною?
6. Дайте означення модуля та аргументу комплексного числа.
7. Що називають головним значенням аргументу?
8. За якою формулою визначається модуль комплексного числа, аргумент комплексного числа?
9. Як виконуються дії над комплексними числами, заданими в алгебраїчній формі?
10. Як виконуються дії над комплексними числами, заданими в тригонометричній формі?
11. Наведіть показникову форму комплексного числа.
12. Як виконуються дії над комплексними числами, заданими в показниковій формі?
13. Який геометричний зміст суми та різниці комплексних чисел?
14. Який геометричний зміст операції множення двох комплексних чисел?
15. Який геометричний зміст операції ділення двох комплексних чисел?
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 16808; Нарушение авторских прав?; Мы поможем в написании вашей работы!