Закон инерции для квадратичных форм

Определения.

1. Квадратичная форма F называется положительно определённой или положительной (F > 0), если " x ¹ 0 F(x)> 0. Тогда и f называется положительно определенной, f > 0.

Очевидно, в этом случае F имеет нормальный вид

F(z) = z₁²+…+z_п², и s = n, t = 0.

2. Аналогично, F - отрицательно определённая или отрицательная (F < 0), если " x ¹ 0 F(x) < 0. Тогда и f < 0.

В этом случае F имеет нормальный вид

F(z) = - z₁²-…- z_п², где s = 0, t = п.

3. Будем говорить, что F неотрицательно определённая

(F ³ 0), если " x ¹ 0 F(x) ³ 0. Тогда и f ³ 0.

Очевидно, в этом случае F имеет нормальный вид

F(z) = z₁²+…+z_s², где s < n, t = 0.

4. Также F - неположительно определённая (F £ 0), если

" x ¹ 0 F(x) £ 0. Тогда и f £ 0, а F имеет нормальный вид

F(z) = - z₁²-…- z_t², где s = 0, t < n.

5. И наконец, F - неопределённая, если $ x такой, что F(x)> 0, и $ у такой, что F(у) < 0. Тогда и f – неопределённая, а F имеет нормальный вид F(z) = z₁²+…+z_s²– z_s+1²-…- z_s+t², где

s > 0, t > 0.

Теорема (закон инерции). Если форма F в базисе е имеет нормальный вид F(z) = z₁²+…+z_s²– z_s+1²-…-z_s+t², то числа s и t от базиса не зависят, то есть для любого базиса е¢, в котором F имеет нормальный вид, числа s и t будут теми же самыми.

Доказательство. Докажем, что s равно максимальной размерности подпространства в L, на котором F > 0. Отсюда и будет следовать независимость s от базиса. Очевидно, если е = {е₁,е₂,…,е_n}, то подпространство L₁ = <е₁,е₂,…,е_s> такое, что 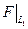> 0. Таким образом, существует подпространство размерности s, на котором F > 0.

Покажем, что не существует подпространства размерности большей s, на котором F > 0. Предположим противное: пусть L₂ – подпространство, на котором F > 0, и dimL₂ > s. Рассмотрим подпространство L₃ = <е_s+1,…,е_n>. Очевидно, 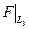£ 0. По теореме 3 из п.12 dimL₂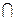L₃ = dimL₂ + dimL₃ – – dim(L₂+L₃) > s + (n – s) – n = 0 Þ если L₂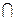L₃ ' х, х ¹ 0, то F(х)> 0 и F(х)£ 0 - противоречие, то есть L₂ не существует, и для s теорема доказана.

Далее рассмотрим форму – F. Теперь числа t и s меняются ролями, и t – это максимальная размерность подпространства в L, на котором – F > 0. То есть t также не зависит от базиса.

ÿ

Определение. Число s называется положительным индексом инерции формы F и обозначается I⁺(F). Число t называется отрицательным индексом инерции формы F и обозначается I ^-(F).

Из доказанной теоремы следует корректность определения индексов инерции.

Следствие. Квадратичные формы имеют 2 числовых инварианта I⁺ = s, I ^- = t, которые независимы и составляют полную систему инвариантов, так как определяют квадратичную форму с точностью до эквивалентности. Другими словами, любой класс эквивалентных квадратичных форм однозначно определяется парой чисел (s, t).

Упражнение. Посчитать количество классов эквивалентных форм.

Дата добавления: 2014-01-04