Метод Монте-Карло

План

Лекція 15 Сутність та організація обліку валютних операцій

Тема 7. Облік операцій в іноземній валюті

1. Організація обліку валютних операцій.

2. Характеристика рахунків для обліку валютних операцій.

3. Облік ведення операцій за рахунками клієнтів в іноземній валюті.

1.Організація обліку валютних операцій.

Згідно з чинним законодавством України, банки мають право здійснювати валютні операції тільки після отримання письмового дозволу (генеральної ліцензії) від НБУ за умови дотримання відповідних спеціальних вимог, які визначаються Положенням про порядок видачі банкам банківських ліцензій, письмових дозволів та ліцензій на виконання окремих операцій (Постанова НБУ №275 від 17.07.01р. Банки можуть отримати письмовий дозвіл на здійснення таких операцій з валютними цінностями:

1. Неторговельні операції з валютними цінностями;

2. Ведення рахунків клієнтів в іноземній валюті;

3. Ведення кореспондентських рахунків банків в іноземній валюті;

4. Залучення та розміщення іноземної валюти на валютному ринку.

Процес відображення в бухгалтерському обліку валютних операцій регламентується Інструкцією з бухгалтерського обліку операцій в іноземній валюті та банківських металах у банках України, затвердженою Постановою Правління НБУ № 555 від 17.11.2004 р. Ця Інструкція визначає основні методологічні засади відображення в бухгалтерському обліку інформації про операції в іноземній валюті та банківських металах, що здійснюють банки України.

Обліковий механізм відображення валютних операцій містить такі структурні елементи:

- облік міжбанківських розрахунків в іноземній валюті;

- облік ведення поточних рахунків клієнтів в іноземній валюті;

- облік міжнародних розрахункових операцій;

- облік обмінних операцій з іноземною валютою;

- облік депозитних та кредитних операцій в іноземній валюті;

- облік операцій з банківськими металами.

Відображення в обліковій системі валютних операцій здійснюється за допомогою тих самих балансових та позабалансових рахунків, що й операції в національній валюті, відповідно до їхнього економічного змісту, оскільки План рахунків бухгалтерського обліку банків України є мультивалютним.

Використання рахунків Плану рахунків забезпечує ведення синтетич­ного обліку валютних операцій. Деталізована інформація про здійснені операції відображається на рівні аналітичного обліку з використанням встановлених НБУ параметрів аналітичних рахунків. Бухгалтерський облік операцій в іноземній валюті здійснюють у подвійній оцінці: в номінальній сумі іноземної валюти та в гривневому еквіваленті за офіційним курсом. Активи і зобов'язання в іноземній валюті і банківських металах у фінансовій звітності відображають в гривневому еквіваленті за офіційним курсом на дату їх визнання.

Доходи і витрати (нараховані, отримані, сплачені) в іноземній валюті в бухгалтерському обліку відображають за рахунками класів 6 і 7 у націо­нальній валюті за офіційним курсом гривні до іноземних валют на дату їх визнання з використанням технічних рахунків групи 380 "Позиція банку щодо іноземних валют та банківських металів".

2.Характеристика рахунків для обліку валютних операцій.

Технічні рахунки - це рахунки, що не несуть економічного навантаження і які використовують для технічного здійснення операцій. Формування фінансової звітності здійснюють без урахування залишків за технічними рахунками.

Рахунок 3800 АП "Позиція банку щодо іноземної валюти та банківських металів" та рахунок 3801 АП "Еквівалент позиції банку щодо іноземної валюти та банківських металів" забезпечують зв'язок між операціями в іно­земній валюті та національній.

Рахунки 3800 та 3801 є активно-пасивними. За дебетом рахунка 3800 відображають вартість іноземної валюти чи банківського металу, що збільшує коротку або зменшує довгу відкриту валютну позицію. За кредитом 3800 відображають вартість іноземної валюти, що збільшує довгу або зменшує коротку відкриту валютну позицію.

За дебетом рахунка 3801 проводять еквіваленти сум іноземної валюти банківських металів, що збільшують довгу або зменшують коротку відкриту валютну позицію. За кредитом рахунка проводять еквіваленти сум іноземної валюти чи банківських металів, що збільшують коротку або зменшують довгу відкриту валютну позицію.

Рахунки валютної позиції (3800) відображають балансові позиції банку і іноземних валютах і банківських металах, а рахунки гривневого еквівалента валютної позиції (3801) - вартість валютних позицій у гривнях.

У кінці кожного операційного дня суми залишків у гривневому еквіва­ленті за технічними рахунками 3800, 3801 мають бути тотожними.

Різницю між сумами залишків у гривневому еквіваленті іноземної валюти та банківських металів за аналітичними рахунками 3800 і 3801 у роз­різі кодів іноземних валют та банківських металів, що виникають через математичне округлення, відображають за балансовим рахунком 6204 АП "Результат від торгівлі іноземною валютою та банківськими металами". Залишки за технічними рахунками 3800 і 3801 не включають до фінансової звітності.

3.Облік ведення операцій за рахунками клієнтів в іноземній валюті.

Уповноважені банки як суб'єкти міжбанківського валютного ринку мають право здійснювати операції з купівлі та продажу іноземної валюти для власних потреб на міжнародному ринку та на валютному ринку України.

Бухгалтерський облік безготівкових обмінних операцій в іноземній ва­люті має свої особливості.

До безготівкових обмінних операцій в іноземній валюті належать:

- операції з купівлі-продажу іноземної валюти на дату операції (за умовами "спот" та "форвард");

- операції з придбання іноземної валюти для власних потреб банку у клієнтів банку на дату розрахунку;

- операції з продажу іноземної валюти для власних потреб банку клієнтам банку на дату розрахунку;

- операції з купівлі іноземної валюти за дорученням клієнтів на дату розрахунку;

- операції з продажу іноземної валюти за дорученням клієнтів;

- операції з купівлі-продажу іноземної валюти на міжнародному ринку та на валютному ринку України.

Уповноважені банки, здійснюючи операції з купівлі-продажу іноземної валюти на дату операції, використовують рахунки позабалансового обліку, оскільки валютна операція на умовах "тод" (сьогодні на сьогодні), "том" (сьогодні на завтра), на умовах "спот" - це валютна операція за договором, умови якого передбачають виконання цієї операції на другий робочий день після дня укладання договору; а валютна операція на умовах "форвард" - це валютна операція за договором, умови якого передбачають виконання цієї операції (з поставкою валюти за договором) пізніше ніж на другий робочий день після дня укладання договору.

Операції з купівлі-продажу іноземної валюти та банківських металів на міжбанківському валютному ринку відображаються в бухгалтерському обліку такими проводками:

1.На дату розрахунку:

а) перерахування гривні на купівлю іноземної валюти та банківських металів:

Д-т 2800, 2900,3540 К-т 1200, 1500, 1600

б) зарахування придбаної іноземної валюти та банківських металів:

Д-т 1500, 1600 К-т 2900, 3640

в) у разі повернення клієнту коштів у національній валюті, якщо іноземна валюта куплена за курсом, нижчим, ніж заявлено клієнтом:

Д-т 2900 К-т 2600, 2620,2650

г) закриття дебіторської, кредиторської заборгованості та визнання резуль­тату від купівлі іноземної валюти та банківських металів:

Д-т 2900, 3640 К-т3800

Одночасно здійснюється бухгалтерська проводка:

Д-т 3801 - на суму гривневого еквівалента іноземної валюти та банківського металу, що купуються

К-т 2800, 3540, 6204 - у разі додатної різниці між гривневим еквівалентом купленої іноземної валюти за офіційним курсом гривні щодо іноземних валют та її вартістю за курсом купівлі

Або:

Д-т 6204 - у разі від'ємної різниці між гривневим еквівалентом купленої іноземної валюти за офіційним курсом гривні щодо іноземних валют та її вартістю за курсом купівлі;

Д-т 3801 - на суму гривневого еквівалента іноземної валюти та банківського металу, що купуються

К-т 2800, 3540

Операції з продажу іноземної валюти та банківських металів за гривні на міжбанківському валютному ринку України відображаються в бухгалтерському обліку на дату розрахунку такими проводками:

а) перерахування суми проданої іноземної валюти та банківських металів:

Д-т 2900, 3540 К-т 1500, 1600

б) отримання суми в гривнях від продажу іноземної валюти:

Д-т 1200, 1500, 1600 К-т 2900, 3640

в) закриття дебіторської, кредиторської заборгованості та визнання результату від продажу іноземної валюти та банківських металів:

Д-т3800

К-т 3540 - на суму проданої іноземної валюти

Одночасно:

Д-т 2900, 3640 - на суму отриманої гривні

К-т 3801, 6204 - у разі додатної різниці між гривневим еквівалентом проданої іноземної валюти за офіційним курсом гривні до іноземних валют та її вартістю за курсом продажу

Або: Д-т 2900, 3640, 6204 - у разі від'ємної різниці між гривневим еквівалентом проданої іноземної валюти за офіційним курсом гривні щодо іноземних валют та її вартістю за курсом продажу

К-т 3801.

Операції з купівлі-продажу іноземної валюти та банківських металів за іншу іноземну валюту на валютному ринку України та на міжнародному рин­ку відображаються в бухгалтерському обліку такими проводками:

а) перерахування іноземної валюти та банківських металів на купівлю іншої іноземної валюти та банківських металів:

Д-т 2800, 2900, 3540 К-т 1500, 1600

б) зарахування придбаної іноземної валюти та банківських металів:

Д-т 1500, 1600 К-т 2900, 3640

в) закриття дебіторської, кредиторської заборгованостей та визнання ре­зультату від купівлі-продажу іноземної валюти та банківських металів:

Д-т 2900, 3640

К-т 3800 - на суму купленої іноземної валюти та банківських металів

Д-т 3800

К-т 2800, 3540 - на суму проданої іноземної валюти та банківських металів.

Одночасно:

Д-т 3801 - на суму гривневого еквівалента іноземної валюти та банківських металів, що купуються

К-т 3801 - на суму гривневого еквівалента іноземної валюти та банківських металів, що продаються

К-т 6204 - у разі додатної різниці між гривневим еквівалентом проданої та купленої іноземної валюти за офіційним курсом гривні щодо іноземних валют.

Відображення в обліку операції з купівлі-продажу іноземної валюти для власних потреб банку

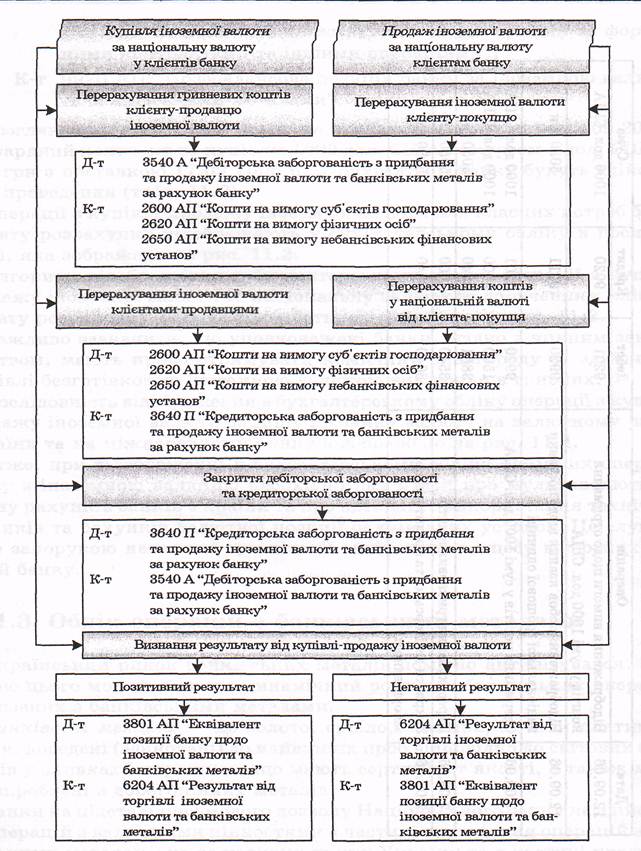
Алгоритм бухгалтерських проведень операцій купівлі-продажу іноземної валюти за дорученням клієнтів

Метод Монте-Карло (за назвою міста Монте-Карло, Монако, яке відоме своїми казино) — загальна назва групи числових методів, основаних на одержанні великої кількості реалізацій стохастичного (випадкового) процесу, який формується у той спосіб, щоб його ймовірнісні характеристики збігалися з аналогічними величинами задачі, яку потрібно розв'язати. Використовується для розв'язування задач у фізиці, математиці, економіці, оптимізації, теорії управління тощо.

Метод Монте-Карло — це метод імітації для приблизного відтворення реальних явищ. Він об'єднує аналіз чутливості (сприйнятливості) і аналіз розподілу ймовірностей вхідних змінних. Цей метод дає змогу побудувати модель, мінімізуючи дані, а також максимізувати значення даних, які використовуються в моделі. Побудова моделі починається з визначення функціональних залежностей у реальній системі. Після чого можна одержати кількісний розв'язок, використовуючи теорію ймовірності й таблиці випадкових чисел.

Метод Монте-Карло широко використовується у всіх випадках симуляції на ЕОМ.

Не існує єдиного методу Монте-Карло, цей термін описує великий і широко використовуваний клас підходів. Проте ці підходи використовують в своїй основі єдиний шаблон:

- визначити область можливих вхідних даних;

- випадковим чином згенерувати вхідні дані із визначеної вище області за допомогою деякого заданого розподілу ймовірностей;

- виконати детерміновані обчислення над вхідними даними;

- проміжні результати окремих розрахунків звести у кінцевий результат.

Наприклад, значення π можна наблизити використанням методу Монте-Карло:

1) намалюйте квадрат на підлозі, а потім вмалюйте коло всередину нього. З геометрії, співвідношення площі вписаною кола до площі зовнішнього квадрата становить π/4;

2) рівномірно розкидати деякі об'єкти однакового розміру по всій площі квадрата. Наприклад, це можуть бути зерна рису;

3) оскільки дві області знаходяться в співвідношенні π/4, об'єкти повинні потрапити в області приблизно в тій же пропорції. Таким чином, підрахувавши кількість об'єктів в колі і розділити на загальну кількість об'єктів в квадраті, отримаємо наближене значення π/4;

4) помноживши результат на 4 буде отримано наближене значення власне самого π.

4. Принципи методу поелементних перевірок

При використанні методу поелементних перевірок система розглядається у вигляді послідовного ланцюжка елементів, вихід кожного з яких призводить до відмови виробу. Для кожного елемента повинні бути відомі дані про надійність і час проведення перевірок.

Ідея методу поелементних перевірок полягає тому, що пошук відмов вузла ведеться шляхом діагностики кожного з елементів у певній, заздалегідь встановленої, послідовності. При виявленні елемента, що відмовив пошук припиняється і проводиться заміна відмовився елемента, а потім перевірка працездатності об'єкта. Якщо перевірка показує, що об'єкт має ще одну відмову, то пошук продовжується з тієї позиції, на якій був виявлений відмовляє елемент. Операція триває, поки не буде виявлений останній несправний елемент.

Основне завдання, яке вирішується при використанні методу послідовних поелементних перевірок, полягає у визначенні послідовності перевірок. При цьому у загальному вигляді розглядається об'єкт, що складається з N елементів, довільним чином з'єднаних між собою, з відомими інтенсивностями відмов l i, i = 1,2,... N. Звичайно передбачається, що непрацездатним може бути тільки один елемент. Відомі також тривалості перевірок кожного елемента t i. Необхідно знайти таку послідовність перевірок, при якій середній час пошуку несправності буде мінімальним.

Для забезпечення мінімального середнього часу пошуку елемента, що відмовив перевірки слід здійснювати відповідно до послідовності a 1 / t 1 <a 2 / t 2 <... <a N / t N, де порядкові номери від 1 до N позначають черговість проведення перевірок.

5. Елементи теорії графів

Теорія графів — розділ математики, що вивчає властивості графів. Останні спрощено можна розглядати як сукупність точок (вершини) сполучених лініями (ребрами). Визначення графу є настільки загальним, що цим терміном можна описувати безліч подій та об'єктів повсякденного життя. Високий рівень абстракції та узагальнення дозволяє використовувати типові алгоритми теорії графів для вирішення зовнішньо несхожих задач у транспортних і комп'ютерних мережах, будівельному проектуванні, молекулярному моделюванні тощо.

Рис. 1. Граф зі шістьма вершинами та сімома ребрами

Картинка у вигляді набору точок на площині та ліній, проведених між деякими з них, стала зручною і наочною формою зображення найрізноманітніших об’єктів, процесів та явищ (див. рис. 1). Два ребра називаються суміжними, якщо вони мають спільну вершину.

Великою мірою це пов’язано з виникненням, бурхливим розвитком та поширенням електронних обчислювальних машин і, як наслідок, значним зростанням ролі задач дискретного характеру. Математика від "обслуговування" переважно фізики переходить до проникнення своїх методів у інші сфери людської діяльності. Одним з потужних інструментів такого проникнення є граф.

Із суто формальної точки зору граф можна розглядати як один з різновидів алгебраїчної системи (а саме, як модель), а отже, і всю теорію графів, як розділ сучасної алгебри. Справді, результати та методи алгебри широко використовуються в теорії графів. Однак за останні півстоліття активного інтенсивного та екстенсивного розвитку теорія графів виробила свою достатньо специфічну власну проблематику і методологію. На сьогодні теорія графів є однією зі складових математичного апарату кібернетики, важливим розділом дискретної математики.

Важливі класи підграфів складають підграфи, які отримуються в результаті застосування до заданого графа операції вилучення вершини і/або операції вилучення ребра.

Останнім часом графи і пов’язані з ними методи досліджень використовуються практично в усіх розділах сучасної математики і, зокрема, дискретної математики.

Граф є математичною моделлю найрізноманітніших об’єктів, явищ і процесів, що досліджуються і використовуються в науці, техніці та на практиці. Коротко опишемо найвідоміші застосування теорії графів.

Наприклад, у вигляді графа можуть бути зображені:

- електричні і транспортні мережі;

- інформаційні і комп’ютерні мережі;

- карти автомобільних, залізничних і повітряних шляхів, газо- і нафтопроводів;

- моделі кристалів;

- структури молекул хімічних речовин;

- моделі ігор;

- різні математичні об’єкти (відношення, частково впорядковані множини, решітки, автомати, ланцюги Маркова, алгоритми і програми тощо);

- лабіринти;

- плани діяльності або плани виконання певних робіт (розклади);

- генеалогічні дерева тощо.

Приклади застосування теорії графів:

- пошук зв’язних компонентів у комунікаційних мережах;

- пошук найкоротших, “найдешевших” та “найдорожчих” шляхів у комунікаційних мережах;

- побудова кістякового дерева: зв’язність з найменшою можливою кількістю ребер;

- пошук максимальної течії для транспортної мережі, в якій визначено вхідні та вихідні вершини та пропускні спроможності ребер;

- ізоморфізм графів: ідентичність структур молекул (ізометрія);

- знаходження циклів графів:

- гамільтонів цикл: обійти всі вершини графа, побувавши в кожній з них лише один раз (задача комівояжера);

- ейлерів цикл: обійти всі ребра (контроль дієздатності мережі);

- розфарбування графів: розфарбування географічних карт, укладання розкладів, розміщення ресурсів тощо;

- планарність графів: проектування друкованих електронних та електричних схем, транспортних розв’язок тощо;

- знаходження центрів графа: вершин, максимальна відстань від яких до всіх інших вершин графа є мінімальною (“столиць”) тощо.

6. Теорія алгоритмів

Теорія алгоритмів як окремий розділ математики, що вивчає загальні властивості алгоритмів, виникла в 30-х роках 20 століття. Алгоритми, проте, простежуються в математиці протягом всього часу її існування. Необхідність точного математичного уточнення інтуїтивного поняття алгоритму стала неминучою після усвідомлення неможливості існування алгоритмів розв’язку багатьох масових проблем, в першу чергу пов'язаних з арифметикою та математичною логікою. Для доведення неіснування алгоритму треба мати його точне математичне визначення, тому після сформування поняття алгоритму як нової та окремої сутності першочерговою стала проблема знаходження адекватних формальних моделей алгоритму та дослідження їх властивостей. При цьому формальні моделі були запропоновані як для первісного поняття алгоритму, так і для похідного поняття алгоритмічно обчислюваної функції.

Для формалізації самого поняття алгоритму були запропоновані точні математичні описи алгоритмічної машини та обчислюваності на ній. Першою формальною моделлю алгоритмічної машини була машина Тюрінга (Алан Тюрінг, Еміль Пост, 1936). Із пізніших моделей відзначимо нормальні алгоритми (А. Марков, І952) та регістрові машини (Д. Шепердсон, Г. Стерджіс, 1963).

Теорія алгоритмів виникла як розділ математичної логіки, поняття алгоритму тісно пов'язане з поняттям числення. Перші та найчисельніші застосування теорія алгоритмів маємо саме в математичній логіці. Теорія алгоритмів є теоретичним фундаментом програмування, вона має застосування всюди, де зустрічаються алгоритмічні проблеми (основи математики, теорія інформації, теорія керування, конструктивний аналіз, обчислювальна математика, теорія ймовірності, лінгвістика, економіка та ін.).

Основні поняття теорії алгоритмів

Областю застосовності алгоритму називається сукупність тих об’єктів, до яких його можна застосувати, тобто в застосуванні до яких він дає результат. Про алгоритм U кажуть, що він:

1) «обчислює функцію f», коли його область застосування збігається з областю визначення f, і U перетворює будь-який х зі своєї області застосування в f(х);

2) «розв’язує множину A відносно множини X», коли він застосовується до будь-якого х з X, і перетворює будь-який х з X∩A на слово «так», а будь-який х з Х\А — на слово «ні»;

3) «перераховує множину B», коли його область застосування є натуральний ряд, а сукупність результатів є B. Функція називається обчислюваною, якщо існує алгоритм, що її обчислює. Множина називається розв’язною відносно X, якщо існує алгоритм, що розв’язує її відносно X. Множина називається перераховуваною, якщо або вона порожня, або існує перераховуючий її алгоритм.

Розв’язні і перераховувані множини складають найпростіші (і найважливіші) приклади множин, структура яких задається за допомогою тих чи тих алгоритмічних процедур. Систематичне вивчення множин конструктивних об’єктів з точки зору таких властивостей цих множин, які зв’язані з наявністю тих чи тих алгоритмів, утворює так звану алгоритмічну теорію множин.

Теорію алгоритмів можна розділити на дескриптивну (якісну) і метричну (кількісну). Перша досліджує алгоритми з точки зору встановлюваної ними відповідності між вихідними даними і результатами; до неї належать, зокрема, проблеми побудови алгоритму, що йому властиві ті чи ті властивості,— алгоритмічні проблеми. Друга досліджує алгоритми з точки зору складності як самих алгоритмів, так і обчислень, що ними задаються, тобто процесів послідовного перетворення конструктивних об'єктів. Важливо підкреслити, що як складність алгоритмів, так і складність обчислень можуть визначатися різними способами. Розробка методів оцінки складності алгоритмів і обчислень має важливе теоретичне і практичне значення.

Теорія алгоритмів тісно зв’язана:

1) з математичною логікою, оскільки в термінах алгоритмів може бути викладено одне з центральних понять математичної логіки — поняття числення;

2) з основами математики, в яких одне з центральних місць займає проблема співвідношення конструктивного і неконструктивного;

3) з кібернетикою, в якій важливе місце займає вивчення алгоритмів керування. Теорія алгоритмів утворює теоретичний фундамент для низки питань обчислювальної математики.

7. Елементи теорії інформації

Теóрія інформáції — це розділ математики, який досліджує процеси зберігання, перетворення і передачі інформації. Теорія інформації тісно пов’язана з такими розділами математики як теорія ймовірностей і математична статистика. Вона пов’язана з інформаційною ентропією, комунікаційними системами, криптографією, корекцією помилок і іншими важливими областями.

Аксіоми теорії інформації:

1. Інформація є лише там, де функціонують пристрої керування.

2. Інформація зберігається і передається тільки на матеріальному носії.

3. Інформація має ідеальний характер.

4. Інформація має різні форми.

Базові закони теорії інформації:

1) на отримання інформації будь-яка кібернетична система витрачає не менше деякої мінімальної кількості енергії;

2) кількість інформації, яку отримує кібернетична система в процесі розпізнавання після прийняття певного сигналу, дорівнює логарифму при основі m від кількості варіантів вибору, що передували розпізнаванню;

3) що меншою є ймовірність завершення якогось випробування з певним результатом, то більше інформації для будь-якої кібернетичної системи несе саме цей результат, і навпаки;

4) будь-які сигнали, отримані кібернетичною системою, впливають на цю систему.

Виникнення теорії інформації зазвичай пов’язують із появою у 1948 р. фундаментальної праці американського вченого Клода Шеннона „Математична теорія зв’язку”. Теорія Шеннона (якого вважають „батьком” теорії інформації), з самого початку розглядалась як точно сформульована математична задача і дала можливість інженерам визначати ємність комунікаційного каналу.

В основі теорії інформації лежить запропонований Шенноном спосіб обчислення кількості інформації як випадкової величини відносно іншої випадкової величини. Для дискретних випадкових величин X і Y, заданих законами розподілу P(X = Xi) = pi,P(Y = Yj) = qj і спільним законом розподілу P(X = Xi,Y = Yj) = pi,j, кількість інформації в X відносно Y, дорівнює

Дата добавления: 2014-01-04