Факторгруппы

Теорема Лагранжа.

Пусть G – группа, и H – подгруппа в G. Введем на множестве G бинарное отношение ~: для элементов g₁, g₂ Î G будем считать по определению, что g₁ ~ g₂ Û g₁g₂^-1Î Н. Выражение g₁g₂^-1 называется групповой разностью.

Очевидно, g₁g₂^-1= h Î Н Û g₁= h g₂.

Утверждение. Отношение ~ является отношением эквивалентности на G.

Доказательство. Очевидно, отношение ~ - рефлексивно, то есть "gÎ G g ~ g, так как g g ^-1 = e Î H. Кроме того, отношение ~ - симметрично, так как если g₁ ~ g₂, то

g₁g₂^-1= h Î Н Þ h ^-1ÎH, h ^-1= g₂g₁^-1Î H Þ g₂ ~ g₁ . И наконец, отношение ~ - транзитивно, так как если g₁~ g₂, g₂ ~ g₃, то g₁g₂^-1= h₁Î Н, g₂g₃^-1= h₂ Î Н Þ h₁h₂ = g₁g₃^-1Î Н Þ g₁ ~ g₃.



Таким образом, множество G разбивается в объединение непересекающихся классов эквивалентных элементов. Причем cl g₁ = {g Î G| g ~ g₁} = {g Î G| g = hg₁, h Î Н } = Hg₁. Класс Hg₁ называется правым смежным классом элемента g₁ по подгруппе Н. Аналогично, левым смежным классом элемента g₁ по подгруппе Н называется подмножество g₁H.

Упражнение. Найти фактормножество G / ~ в случаях, когда H = G и H = {e}.

Пусть G – конечная группа, и число элементов группы G равно п: |G| = n. Число элементов группы называется порядком группы. Пусть Н – подгруппа в G, |H| = m.

Теорема Лагранжа. m | n, причем n = km, где k – число правых смежных классов группы G по подгруппе Н.

Доказательство. Пусть H = { h₁,…, h_m}. Тогда

Hg ={ h₁g,…, h_mg }, причем все элементы h₁g,…,h_mg – различ-

ны, так как если h_ig = h_jg, то h_igg ^-1 = h_jgg ^-1 Þ h_i = h_j. Следовательно, | Hg| = m = |H|, то есть число элементов во всех правых смежных классах одинаково и равно т. Так как количество смежных классов равно k, они не пересекаются и их объединение совпадает с G, то n = mk Þ m = n / k.



Аналогично доказывается теорема Лагранжа для левых смежных классов группы G по подгруппе Н. И количество их также равно n / k = т.

Определение. Количество смежных классов (правых или левых) группы G по подгруппе Н называется индексом подгруппы Н в группе G и обозначается (G:H).

В новых обозначениях теорема Лагранжа может быть сформулирована так: |G| / |H| = (G:H).

Пусть G – произвольная, не обязательно конечная группа.

Замечание. Так как " a, bÎ G (ab)(b ^-1a ^-1)= a(bb^-1)a ^-1 =

= aea ^-1 = e, то (ab) ^-1 = b ^-1a ^-1.

Теорема. Для подгруппы H Ì G эквивалентны следующие 4 условия:

1. " h Î H, " g Î G g ^-1hg Î H;

2. " g Î G g ^-1Hg Í H;

3. " g Î G g ^-1Hg = H;

4. " g Î G Hg = gH – то есть правые и левые смежные класы совпадают.

Доказательство. Очевидно, 1 Û 2 – это одно и то же условие, записанное в 1 для элементов, а в 2 для множеств. Также очевидно, что 3 Þ 2. Покажем, что 2 Þ 3. Заменим в условии 2 элемент g на g^-1. Получим gHg ^-1Í H. Умножим это включение слева на g ^-1 и справа на g. Получим HÍ g^-1Hg. Это включение вместе с включением из 2 дает равенство 3. Следовательно, 2 Û 3. И наконец, равенство 4 получается умножением равенства 3 на g слева, а равенство 3 получает-

ся умножением равенства 4 на g ^-1 справа. То есть 3 Û 4.

Определение. Подгруппа H Ì G называется нормальной

подгруппой (или нормальным делителем) в G, если для Н выполняется любое из четырёх эквивалентных условий теоремы (а, следовательно, и все четыре условия).

Очевидно, в коммутативной группе любая подгруппа – нормальная.

В случае нормальной подгруппы Н фактормножество G/~

мы будем обозначать G / H. В этом случае левые и правые смежные классы совпадают, и их можно просто называть смежными классами. Обозначать смежный класс элемента g мы будем .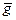

Очевидно, тривиальные подгруппы {e} и G – нормальны.

Пусть Н – нормальная подгруппа в G. Зададим на фактормножестве G / H структуру группы.

I. Пусть для 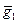, 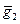Î G/H по определению ×= .

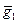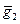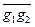Утверждение. Определение умножения на G/H коррект-

но, то есть не зависит от выбора представителей в классах 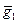и .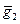

Доказательство. Пусть g₁¢Î 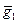, g₂¢Î 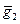- другие представители в классах. Покажем, что g₁¢g₂¢ Î 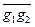, то есть g₁¢g₂¢ ~ g₁g₂. В самом деле, g₁¢ ~ g₁ , g₂¢ ~ g₂ Þ g₁¢ = h₁g₁, g₂¢= h₂g₂ Þ g₁¢g₂¢= h₁g₁h₂g₂=h₁g₁h₂(g₁^-1g₁)g₂= h₁(g₁h₂g₁^-1)g₁g₂= = h₁h¢g₁g₂ = h¢¢g₁g₂, и h¢¢Î H Þ g₁¢g₂¢ ~ g₁g₂, = .



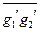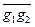II. Проверим свойства из определения группы.

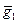
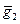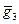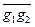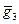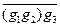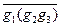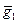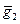
1. ( ) = ×= = = (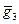) – ассоциативность в G / H выполняется.

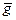
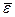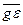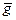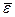
2. = = = 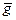, то есть в G / H $ нейтральный элемент .

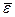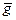
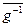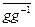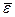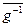
3. Очевидно, = = = 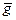, то есть в G / H

для элемента 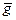$ обратный элемент 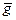^-1 = .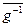

Таким образом, на фактормножестве G / H мы задали

структуру группы, которая называется факторгруппой.

Дата добавления: 2014-01-04