Основні означення

У загальному випадку проста регресійна модель має вигляд:

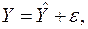(16.1)

де 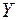– вектор спостережень, що відповідає незалежній випадковій величині (внутрішній фактор системи):

;

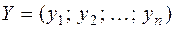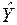– вектор значень функціонального фактора відповідно до моделі:

, (16.2)

де– функція, за якою здійснюється апроксимація стохастичної залежності, або тренд, тобто тенденція зміни функціонального фактора;

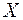– вектор спостережень, що відповідає незалежній змінній, який у термінах регресійного аналізу ще має назву регресора:

;

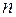– загальна кількість спостережень (обсяг вибіркової сукупності);

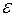– вектор похибок моделі:

.

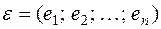Оскільки рівняння регресії відображає теоретичні уявлення про зв’язок між ознаками та 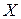, то значення, що обчислені відповідно до математичної моделі (16.2), треба відрізняти від емпіричних значень функціонального фактора, тому результати обчислення мають позначку ^.

Однією з передумов застосування як кореляційного, так і регресійного аналізів є нормальний розподіл кожної з випадкових величин 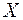і .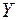

Найбільш простою і водночас найбільш поширеною є лінійна модель кореляційного зв’язку. Крім того, в багатьох випадках нелінійний зв’язок між випадковими величинами 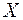та 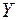також можна перетворити на лінійний шляхом або безпосередньої заміни змінних, або попереднього логарифмування рівняння з подальшою заміною змінних. Так, легко лінеаризуються двопараметричні залежності наступних типів:

, , , ,

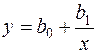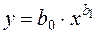тощо, які достатньо часто зустрічаються в економічних дослідженнях. Навіть у тому випадку, коли лінію регресії в цілому не можна апроксимувати однією функцією, її поділяють на відрізки, для кожного з яких апроксимацію проводять окремо. Тобто маємо ламану лінію, кожний відрізок якої характеризується своїм рівнянням регресії, і в цьому випадку зазвичай приймається лінійна залежність між факторами.

Апроксимацією кореляційної залежності для випадку парної лінійної регресії є функція, яку прийнято надавати у вигляді:

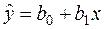, (16.3)

де 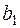– кутовий коефіцієнт лінії тренда, що є статистичною оцінкою коефіцієнта регресії 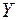на 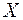у генеральній сукупності;

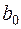– точкова оцінка вільного члена рівняння регресії, що відповідає генеральній сукупності.

У свою чергу, значення параметрів у рівнянні регресії (16.3) теж є результатами обчислення за вибірковою сукупністю, тобто є оцінками параметрів теоретичного рівняння регресії. Щоб підкреслити цю особливість, статистичні оцінки параметрів теж мають позначку ^. Отже, матриця 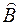, елементами якої є коефіцієнти рівняння (16.3), є матрицею статистичних оцінок параметрів теоретичного рівняння регресії.

Аналогічно визначається рівняння тренда у випадку парної лінійної регресії 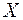на :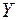

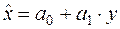, (16.4)

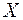де – кутовий коефіцієнт лінії тренда, який є точковою оцінкою коефіцієнта регресії на ;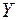

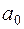– точкова оцінка вільного члена рівняння регресії, що відповідає генеральній сукупності.

Вибіркові рівняння регресії (16.3) і (16.4) є рівняннями, що подані в натуральних змінних. Ці рівняння також зручно надавати в симетричній формі:

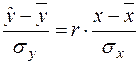та . (16.5)

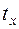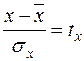Вирази, які містяться у лівій та правій частинах цих рівнянь, можна розглядати як нормовані й стандартизовані випадкові величини, як позначаються, відповідно, та :

та .

Відносно стандартизованих змінних спряжені рівняння регресії набувають вигляду:

та 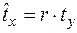. (16.6)

Слід зазначити, що для стандартизованих змінних їх вибіркова середня дорівнює нулю, а дисперсія – одиниці, тобто при розподілі за нормальним законом функцією щільності ймовірностей у генеральній сукупності для цих змінних є функція Гаусса 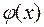, а функцією розподілу – функція Лапласа .

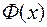Якщо розглядати рівняння парної регресії у формі (16.5), то стає зрозумілим сенс коефіцієнта кореляції. Так, якщо випадкова величина 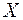збільшується відносно своєї вибіркової середньої на величину 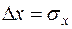, то функціональний фактор за рівнянням тренда матиме приріст, що становить , тобто . Отже, коефіцієнт кореляції визначає, на яку частку від свого середнього квадратичного відхилення змінюється випадкова величина 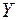, якщо випадкова величина 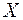змінюється на величину свого середнього квадратичного відхилення.

Оскільки значення факторів 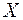і 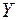, що утворюють вибіркову сукупність , , 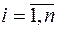є емпіричними значеннями випадкових величини, то при визначенні параметрів моделі нема сенсу вимагати повної відповідності між значеннями, що отримані за теоретичним рівнянням регресії, та емпіричними даними для всіх без винятку точок , 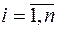. Вид функції 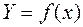вибирають відповідно до теоретичного припущення про характер зв’язку між факторами або за виглядом емпіричних ліній регресії. З урахуванням цих уточнень задача регресійного аналізу полягає в тому, щоб визначити функцію у вигляді 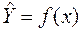, яка в при значеннях аргументу відповідно приймає значення 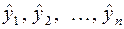, що найбільш близькі до емпіричних даних. Для розв’язання цієї задачі може використовуватись кілька методів, серед яких найбільш поширеним є метод найменших квадратів.

Дата добавления: 2014-01-04