
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод найменших квадратів
|
|
|
|
Метод найменших квадратів (МНК) є одним із методів регресійного аналізу, який використовується для статистичного оцінювання параметрів регресійної моделі за емпіричними даними. Згідно з цим методом параметри моделі повинні відповідати такому рівнянню регресії, що забезпечує найменше значення суми квадратів відхилень емпіричних даних від тих, що обчислені за рівнянням регресії. Так, з двох різних наближень тієї ж самої емпіричної функції, що задана у вигляді таблиці, кращим вважається те, для якого сума квадратів відхилення має найменше значення. Для ілюстрації суті методу найменших квадратів можна розглянути рис. 16.1.

Рис. 16.1. Ілюстрація методу найменших квадратів
Графік функції проходитиме таким чином, щоб різниця між значеннями функції 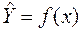 та ординатами емпіричних точок була б якомога менше.
та ординатами емпіричних точок була б якомога менше.
Основи метода найменших квадратів були розроблені Карлом Фрідріхом Гауссом у зв’язку з задачами, що вирішуються теорією помилок, тобто математичною теорією, яка досліджує точність результатів вимірювань. До речі, Гаусс настільки ретельно провів дослідження нормального розподілу випадкових похибок, що їх крива щільності ймовірностей має назву гауссіани.
Узагальнення умов застосування методу найменших квадратів сформульовано у теоремі Гаусса – Маркова.
Теорема Гаусса – Маркова. Якщо прийняти припущення моделі:
1. 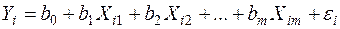 , де
, де 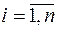 ,
, 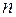 – обсяг вибірки (кількість емпіричних точок);
– обсяг вибірки (кількість емпіричних точок);
2.  – детермінована величина (у загальному випадку це матриця результатів
– детермінована величина (у загальному випадку це матриця результатів 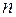 спостережень
спостережень 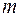 -вимірної випадкової величини
-вимірної випадкової величини 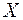 , що відповідає сукупності зовнішніх факторів);
, що відповідає сукупності зовнішніх факторів);
3. 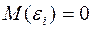 ,
,  , де
, де 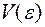 – матриця коваріацій (попарних варіацій) похибок,
– матриця коваріацій (попарних варіацій) похибок,  – похибка
– похибка  -го вимірювання;
-го вимірювання;
4. 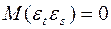 при
при 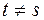 , де
, де 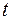 і
і  – номери вимірювань,
– номери вимірювань,
то оцінки параметрів 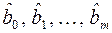 , які отримані за МНК, мають найменшу дисперсію серед усіх лінійних незсунутих оцінок, тобто ці оінки є ефективними.
, які отримані за МНК, мають найменшу дисперсію серед усіх лінійних незсунутих оцінок, тобто ці оінки є ефективними.
Розглянемо сенс кожної з умов теореми Гаусса – Маркова.
Умова 1 визначає специфікацію моделі, тобто кількість факторів, що розглядаються в межах моделі, і форму зв’язку між ними.
Умова 2 уточнює, яка саме випадкова величина є зовнішнім (екзогенним) фактором моделі.
Умова 3 означає, що математичне сподівання помилки дорівнює нулю, а дисперсія помилок є сталою величиною, тобто не залежить від номера спостереження. Остання властивість має назву гомоскедастичності.
Умова 4 вказує на некорельованість помилок різних спостережень. Якщо ця умова порушується, то виникає автокореляція залишків.
Моделі, які побудовані з використанням методу найменших квадратів при виконанні умов теореми Гаусса – Маркова, називаються класичними економетричними моделями, а сам метод їх побудови називається 1МНК, тобто однокроковий метод найменших квадратів.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 21218; Нарушение авторских прав?; Мы поможем в написании вашей работы!