Оцінювання параметрів моделі за методом МНК

Розглянемо застосування методу найменших квадратів до визначення параметрів рівняння регресії на прикладі системи двох випадкових величин 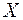і 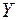, тобто так званий випадок парної регресії.

Для лінійної моделі маємо умовне рівняння:

. (16.7)

За методом 1МНК складемо функцію суми квадратів нев’язок:

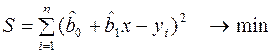
та знайдемо її частинні похідні за невідомими оцінками параметрами і 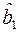, які відповідно до необхідної умови екстремуму повинні дорівнювати нулю. У результаті отримуємо систему рівнянь:

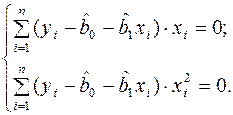
Після перетворень система нормальних рівнянь набуває вигляду:

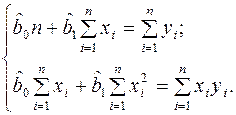(16.8)

Якщо кожне рівняння поділити на обсяг вибіркової сукупності 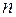, то отримуємо систему нормальних рівнянь, коефіцієнтами якої є оцінки основних числових характеристик двовимірної випадкової величини:

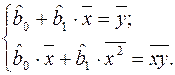(16.8^І)

Цю ж систему можна записати в матричній формі.

Отже, отримуємо рівняння:

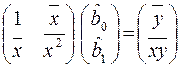, (16.9)

де відповідно до означень

; ;

; .

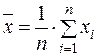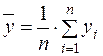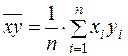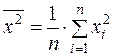Розв’язуючи рівняння (16.9) відносно невідомих параметрів за методом оберненої матриці, маємо:

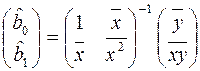, (16.10)

де , 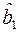– статистичні оцінки параметрів рівняння парної лінійної регресії, або МНК–оцінки.

Оцінки параметрів рівняння регресії, що отримуємо за 1МНК, відповідають усім вимогам до статистичних оцінок, а саме: незсунутість, спроможність та ефективність.

Надання оцінок параметрів регресійної моделі у формі (16.10) фактично означає, що для розв’язання системи нормальних рівнянь (16.8^І) було застосовано метод оберненої матриці. Згідно з означенням оберненої матриці співвідношення (16.10) набуває вигляду:

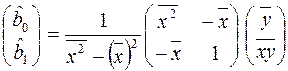. (16.11)

За співвідношенням (16.11) знаходимо параметр :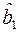

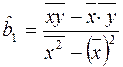
або, приймаючи до уваги означення вибіркового коефіцієнта кореляції, отримуємо:

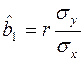. (16.12)

Значення можна також визначити за співвідношенням (16.11), однак після того, як знайдено значення параметра 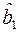, зручно скористатись наступними міркуваннями. Оскільки координати точки 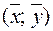, тобто центра вибіркової сукупності, повинні задовольняти рівняння регресії, то для визначення статистичної оцінки параметра маємо співвідношення:

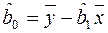. (16.13)

Приклад. Вибіркова сукупність містить дані щодо значень внутрішнього фактора 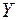залежно від рівня значущості зовнішнього (детермінованого) фактора 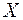, які надані у вигляді таблиці (табл. 16.1).

Таблиця 16.1

Дата добавления: 2014-01-04