Ентропія й ймовірність

Стан системи, що характеризується макропараметрами (p,V,T,U...), називається макростаном. Стан макросистеми, при якому задані стани всіх молекул, називається мікростаном. Будь–який макростан системи може бути реалізовано різними мікростанами. Статистичною вагою макростану називається число можливих мікростанів, що відповідають даному макростанові. Дослід показує, що представлена сама собі макросистема намагається переходити від менш ймовірного стану до більш ймовірного, при цьому ймовірність стану прямо пропорційна статистичній вазі: Р~W. Оскільки при переході від менш до більш ймовірних станів зростає і ентропія, то очевидно припустити, що ентропія пропорційна статистичній вазі. Больцман вивів залежність між ентропією і статистичною вагою:

.

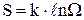Отримана формула називається формулою Больцмана. Принцип зростання ентропії привів Больцмана до висновку: усі замкнуті макросистеми намагаються переходити від станів менш ймовірних до більш ймовірних, при цьому ентропія характеризує ступінь безладдя в макросистемі.

Подальші дослідження показали, що статистика Больцмана є наближеною. Більш точний опис макросистем можна одержати з використанням законів квантової фізики, у якій мікропараметри не можуть приймати будь–які значення. Величини, що характеризують мікрочастинки, можуть приймати тільки дискретні значення, кратні деякої const. Відповідно до квантової теорії всі мікрочастинки підрозділяють на два класи, яким відповідають дві квантові статистики:

- частинки з напівцілим спіном, їх називають ферміонами; вони підкоряються статистиці Фермі–Дірака;

- частинки з цілим спіном – бозоны; вони підкоряються статистиці Бозе–Ейнштейна.

В усіх статистиках припустимі мікростани вважаються рівноймовірними. Їх відмінність полягає у способах визначення мікростанів і статистичних ваг. У статистиці Больцмана вважається, що навіть тотожні частинки принципово помітні. У квантових же статистиках, навпаки, вважається, що тотожні частинки принципово нерозрізнені.

В основу статистики Фермі–Дірака покладений принцип Паулі, згідно якого в кожнім квантовому стані може знаходитися не більш однієї частинки. За статистикою Бозе–Ейнштейна в кожнім стані може знаходиться будь–як число частинок.

Основна задача квантових статистик – це знаходження відповідних їм функцій розподілу частинок по тих або інших параметрах (наприклад, по енергіях), а також визначення середніх значень цих параметрів, що характеризують найбільш ймовірний макростан усієї системи частинок.

Для опису стану системи частинок розглядають уявлюване шестивимірний простір, кожна точка якого характеризується шістьма координатами: х, у, z, р_х, р_у, р_z. Цей простір називають фазовим. Стан системи визначається тим, як розподілені в цьому просторі точки, що зображують стани всіх N частинок системи. При цьому потрібно врахувати властивий частинкам корпускулярно–хвильовий дуалізм, відповідно до якого невизначеності координати х і відповідної проекції імпульсу р_х можуть бути визначені тільки з невизначеністю 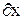і 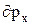, добуток яких, відповідно до принципу невизначеностей Гейзенберга, , де h – стала Планка. Даному станові частинки у фазовому просторі відповідає не точка, а фазова комірка, об’єм якої:

.

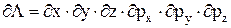Квантові розподіли являють собою функції , що визначають середні числа частинок в одній фазовій комірці з енергією . Для ферміонов:

.

Для бозонов:

,

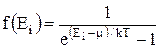де m – хімічний потенціал, що визначається як деяка характерна енергія, значення якої можна знайти з умови нормировки: сумарне число частинок у всіх фазових комірках повинне дорівнювати повному числу N частинок макросистеми.

Особливості розподілів:

- для ферміонов функція не може бути більше одиниці, а для бозонів її значення може бути будь яким;

- якщо 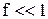, то в знаменниках обох розподілів можна одиницею знехтувати, і формула приймає вигляд:

,

тобто одержуємо розподіл Больцмана (А – нормувальний коефіцієнт). Виходить, що класичний розподіл Больцмана справедливий лише тоді, коли малі «числа заповнення» фазових комірок;

- у макросистемі рівні енергії частинок квазібезперервні (розташовані дуже густо);

- для бозонів значення m не можуть бути позитивними, інакше при виявиться, що f < 0, а це позбавлено фізичного змісту. Для ферміонів подібного обмеження не існує.

Визначимо число dZ фазових комірок в інтервалі енергій (Е, Е + dЕ). Для цього знайдемо спочатку відповідний об’єм dL фазового шестивимірного простору. Виділимо в імпульсній частині фазового простору кульовий шар радіусом, що дорівнює імпульсу р частинки, і товщиною dp. Його об’єм дорівнює 4pp²dp. Помноживши його на відповідний об’єм V координатної частини фазового простору, одержимо шуканий елемент об’єму dL фазового простору:

.

Число dZ фазових комірок у цьому елементі об’єму одержимо, розділивши dL на об’єм однієї фазової комірки h³:

.

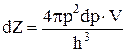Знаючи число dZ фазових комірок в інтервалі енергій (E, E + dЕ), і середнє число частинок у кожній комірці, тобто функцію заповнення f, ми можемо знайти число частинок dn у даному інтервалі енергій:

,

де g – числовий коефіцієнт порядку одиниці, який зв’язаний зі специфікою частинок ідеального газу.

Дата добавления: 2014-01-04