Математичні моделі дискретних каналів

Математичні моделі неперервних каналів.

Характеристики каналів.

Тема: Швидкість передачі інформації і пропускна здатність дискретного та неперервного каналів.

Зміст

Пропускною здатністю каналу називають найбільше значення швидкості передачі інформації каналом зв'язку; вона вимірюється у дв.од./с або біт/с і визначається за формулою: С_к= max R_k.

Тут під швидкістю передачі інформації розуміють середню кількість інформації що надходить із виходу каналу за одиницю часу; вимірюється у дв.од або біт/с. В ідеальному каналі без завад і спотворень кількість прийнятої інформації тотожно дорівнює кількості переданої інформації. Тому швидкість передачі інформації R_K ідеальним каналом дорівнює продуктивності джерела і відповідає інформаційним параметрам первинного сигналу.

В каналі зв'язку із завадами через помилки передачі виникають втрати інформації - деяка її частина не доходить до споживача бо втрачається в каналі. Швидкість передачі інформації дискретним каналом з розрахунком втрат:

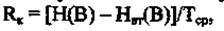
де Н(В) - ентропія дискретного первинного сигналу; Н„(В), - ентропія втрат інформації в каналі; Т_ср - середня тривалість дискретного первинного сигналу. Пропускна здатність дискретного каналу С_к, яким передається m дискретних сигналів, обчислюється за формулою:

Де T_mm - мінімальна тривалість сигналу; р - імовірність помилки сигналів у каналі.

Пропускна здатність двійкового каналу C_g (m = 2), отже: C_g = В [1 +p·log2 p + (1 - р) 1оg(1 - р)], де В = 1/Т_min,- швидкість модуляції, Бод.

Визначимо пропускну здатність двійкового каналу, прийнявши швидкість модуляції в каналі В = 1/τ_с = 1/69,5·10^-6 =1,44·10⁴ Бод, імовірність помилки р=0,1. Згідно з виразом для двійкового каналу, його пропускна здатність при заданих параметрах C_g = 1,44·10⁴ (1 + 0,1·lоg 0,1 + 0,9·log₂ 0,9) = 1,44·10⁴ (1-0,47) = 7,632·10³біт/с.

Для ідеального каналу при р = 0 C_g = В = 1,44·10⁴ біт/с. Порівняння одержаних результатів показує, що помилки в каналі призвели до зменшення пропускної здатності на 47% або на 6,768·10³ біт/с.

Основна теорема кодування Шеннона для каналу з завадами для дискретного каналу формулюється так: якщо продуктивність джерела повідомлень R_д менша за пропускну здатність каналу С_к, тобто R, < С_к то існують способи кодування та декодування, при яких імовірність помилки декодування може бути безмежно малою. Якщо ж R_д ≥ С_к, то таких способів кодування та декодування не існує.

Для неперервних каналів формулювання теореми таке саме, але під помилкою декодування слід розуміти середньоквадратинну похибку (різницю між переданим та прийнятим сигналами). Згідно з теоремою Шеннона, помилки в каналі не є перешкодою для безпомилкової передачі інформації. Помилки дещо зменшують пропускну здатність каналу (див. приклад), але за умови R_д<C_K належними способами кодування та декодування їх усі можна виправити.

Пропускна здатність неперервного гаусового каналу визначається за формулою Шеннона:

де F_K - ширина смуги частот каналу; P_s, P₃ - середні потужності сигналу та завади у смузі частот каналу.

Приклад. Обчислити пропускну здатність неперервного гаусового каналу при F_K = 3100 Гц; P_s =32 мкВт, P_з= 8,7·10^-8 Вт.

Розв'язок. За формулою Шеннона C_KН= F_Klog2 (1 + P_s/Р₃) = 3100·lоg (1 + 32·10⁶/8.7·10^-8) = 26,4-10³ біт/с.

Приклад. Розрахувати С_KH, вважаючи, що в каналі використовується частотна модуляція і тому F_kЧМ =5/τ_с = 5/69,5·10^-6 =7,19·10⁴ Гц, P_s = а²/2= 71/2 = 35,5 В², а також для завади типу теплового (білого) шуму Р₃ = No·F_K = 1,3·10^-3 х 7,19·10⁴ = 93,47В².

Дата добавления: 2014-01-04