
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЛЕКЦІЯ 4. Тема: Числові функції. Визначення числової функції
|
|
|
|
Тема: Числові функції. Визначення числової функції. Способи задання функції. Пряма і обернена пропорційність, їх властивості і графіки. Лінійна функція, її графік.
| Викладач: Пєрмінова І.О. |
| Розглянуто на засіданні предметної (циклової) комісії викладачів | ||
фізико-математичних дисциплін
Протокол № 10 від 10 червня
Голова предметної (циклової) комісії: |
_____________ Н.В.Назаренко
м. Берислав,
2009 р.
Тема лекції: Числові функції. Визначення числової функції. Способи задання функції. Пряма і обернена пропорційність, їх властивості і графіки. Лінійна функція, її графік.
Знати:
- визначення числової функції;
- способи задания функції;
- властивості функції.
Вміти:
- будувати графіки функцій;
- визначати властивості функцій.
Тип лекції: тематична
Ключові поняття: функція, область визначення функції, область значення функції, пряма пропорційність, обернена пропорційність, лінійна функція, графік функції.
План
1. Поняття функції.
2.Способи задання функції.
3. Пряма і обернена пропорційності, їх властивості і графіки.
4. Лінійна функція, її графік
Основна література
1. Кухар В.М., Білий Б.М. Теоретичні основи початкового курсу математики: Навч. посібник для педучилищ. – К.: Вища школа, 1987. – 319 c.
2. Стойлова Л.П., Пишкало А.М. Основы начального курса математики: Учеб. пособие для учащихся педучилищ. – М.: Просвещение, 1988. – 320 c.
Структура лекції
1. Вступна частина:
Оголошення теми, мети і завдань лекції.
Ознайомлення з планом лекції, основною та додатковою літературою.
2. Виклад лекційного матеріалу (згідно плану та вимог до лекції).
І. Поняття функції.
Означення. Функція - це залежність змінної у від змінної х, при якій кожному значенню змінної х відповідає єдине значення у.
y = f (x)
y = x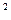 + 25
+ 25
Змінну х називають незалежною змінною (аргументом), а змінну у - залежною змінною (функцією). Говорять також, що у є функцією від х.
f, g, h... – функції
Означення. Область визначення функції (D (y)) – множина значень, яких набуває незалежна змінна х.
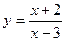 , D (y) = R, крім 3
, D (y) = R, крім 3
Означення. Область значень функції (E (y)) – множина значень залежної змінної у, яких вона набуває при всіх значеннях х.
Означення. Числова функція – це функція, в якої область визначення і множина значень є числові множини.
ІІ. Способи задання функції.
Способи задання функції:
- Аналітичний (за допомогою формулою). Н.:
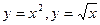 .
. - Табличний (за допомогою таблиці). Н.:
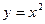
| х | ||||
| у |
- Словесний (переліком пар).
- Графічний (за допомогою графіка).
Графік функції – це зображення на координатній площині множини упорядкованих пар. Прямі Ох і Оу взаємно перпендикулярні, О – точка перетину цих прямих і початок координат. Ох – вісь абсцис, Оу – вісь ординат
ІІІ. Пряма і обернена пропорційності, їх властивості і графіки.
Пряма пропорційність
Означення. Лінійну функцію, що задається формулою y = kx, де k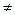 0 називають прямою пропорційністю.
0 називають прямою пропорційністю.
Графіком є пряма, що проходить через початок координат. Якщо k > 0, графік лежить у І і ІІІ координатних чвертях, якщо k < 0, то графік лежить у ІІ і ІV чвертях.
Прямопропорційні залежності: якщо значення змінної х зростають, то зростають і значення змінної у.
Приклад S = V · t, t – const, V – збільшується і S – збільшується.
Обернена пропорційність
Означення. Функція задана формулою 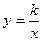 , де х – незалежна змінна, k
, де х – незалежна змінна, k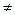 0 – дане число називається обернена пропорційність.
0 – дане число називається обернена пропорційність.
Графіком є гіпербола, яка складається з двох віток. Якщо k > 0, то вітки гіперболи лежать у І і ІІІ чвертях, якщо k < 0, то у ІІ і ІV чвертях.
Властивості:
1. Область визначення: D (y) = R, крім 0.
2. Область значень: Е (y) = R, крім 0.
3. Якщо k > 0 – функція спадає, якщо k < 0 – функція зростає.
4. Функція непарна.
Приклад:  , S – const, t – зменшується, V – збільшується.
, S – const, t – зменшується, V – збільшується.
ІV. Лінійна функція, її графік.
Означення. Лінійною називається функція, яку можна задати формулою y = kx + b, де х – аргумент, k і b – дані числа.
Графіком цієї функції є пряма.
Через дві точки можна провести одну й тільки одну пряму, тому для побудови графіка лінійної функції досить знати координати двох його точок.
Властивості:
1. Область визначення: D (y) = R.
2. Якщо k > 0 – функція зростає, якщо k < 0 – функція спадає.
3. При k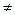 0, b
0, b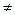 0 – лінійна функція не є ні парною, ні непарною.
0 – лінійна функція не є ні парною, ні непарною.
4. b – ордината точки перетину графіка з віссю Оу.

 у
у
k > 0
 |
х
k < 0
3. Заключна частина:
Загальний висновок.
Відповіді на запитання студентів.
Д/з: Стойлова Л.П., Пишкало А.М. Основы начального курса математики, § 16, п. 99 – 103, впр. 5, 7 (С. 265), 1 (С. 271), 2 (С. 277).
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 812; Нарушение авторских прав?; Мы поможем в написании вашей работы!