Функція Гріна для областей на площині

Функція Гріна для областей у двовимірному випадку в принципі можна будувати в той же спосіб, що і в тривимірному випадку. При цьому треба враховувати вигляд фундаментального розв’язку для 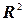, що приводить до наступного вигляду функції Гріна

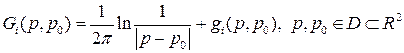(4.14)

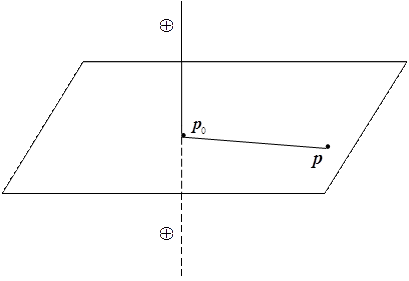Фізичний зміст фундаментального розв’язку в двовимірному випадку представляє собою потенціал електростатичного поля в точці рівномірно зарядженої одиничним додатнім зарядом нескінченої нитки, яка проходить ортогонально до площини через деяку точку 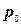. Точки 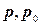належать площині.

Аналогічно кулі, можна отримати функцію Гріна задачі Дірихле для кола, яка має вигляд:

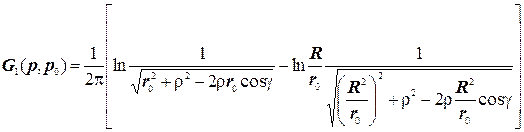(4.15)

Або через комплексні змінні ,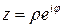

(4.15’)

Таким чином розв’язок задачі Дірихле для кола може бути записана у вигляді:

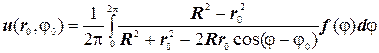(4.16)

Або через точки комплексної площини, ,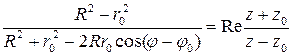

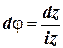
Тоді, формула (4.16) має вигляд

(4.15’)

Нехай необхідно побудувати функцію Гріна першої граничної задачі

(4.17)

для довільної однозв’язної області 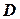з жордановою границею . Якщо відома функція , яка здійснює конформне відображення області 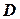на одиничний круг , тоді функція Гріна першої граничної задачі для області 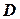буде мати вигляд:

(4.18)

А розв’язок задачі Дірихле (4.17) можна записати у вигляді:

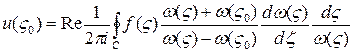(4.19)

Дата добавления: 2014-01-04