Гармонічні функції та їх властивості

Таким чином, фундаментальний розв’язок оператора теплопровідності представляє собою функцію, що моделює температуру стрижня в точці в момент часу за рахунок дії миттєвого точкового джерела інтенсивності яке діє в початковий момент часу в точці.

Для побудови функції Гріна граничних задач (4.20), (4.21) на півпрямій використаємо метод відображення теплових джерел.

Якщо на прямій розташувати в довільній точці 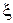миттєве точкове джерело, яке діє в момент часу 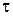інтенсивності 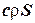, а симетричній точці 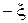миттєве точкове джерело, яке діє в момент часу 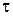і має інтенсивність 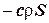, то з фізичних міркувань можна очікувати, що в точці 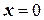, яка лежить посередині між точками 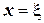та 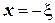, вплив теплових джерел дає нульову температуру. Дійсно, виходячи з фізичного змісту фундаментального розв’язку, отримаємо, що температура від дії двох точкових джерел дорівнює

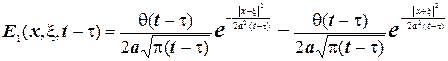(4.22)

Легко перевірити, що 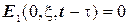, , 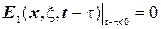а другий додаток 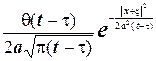задовольняє однорідному рівнянню теплопровідності при 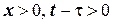. Таким чином 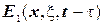є функція Гріна першої граничної задачі рівняння теплопровідності для півпрямої.

Якщо на прямій розташувати в довільній точці 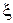миттєве точкове джерело, яке діє в момент часу 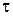інтенсивності 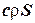, а симетричній точці 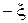миттєве точкове джерело, яке діє в момент часу 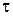і має інтенсивність 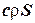, то з фізичних міркувань можна очікувати, що в точці 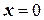, яка лежить посередині між точками 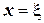та 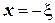, тепловий потік буде дорівнювати нулю.

Запишемо температуру в цьому випадку

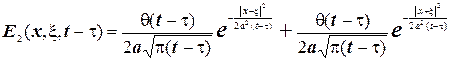(4.23)

Легко перевірити, що ,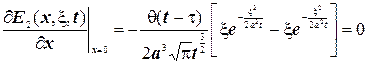

Таким чином 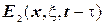є функцією Гріна другої граничної задачі рівняння теплопровідності для пів прямої.

Для запису розв’язку граничних задач (4.20), (4.21) будемо використовувати формули (3.22) та (3.23), які треба записати для випадку пів прямої

Для першої граничної задачі будемо мати:

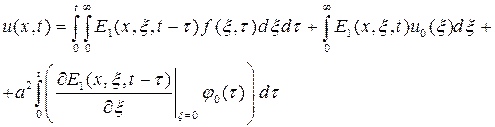(4.24)

Для другої граничної задачі отримаємо

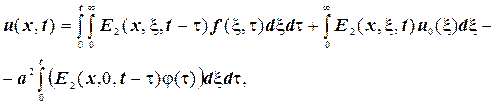(4.25)

Продемонстрований метод це лише один з прийомів, який використовується для побудови функції Гріна.

Означення 1 Функцію 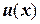називають гармонічною в деякій відкритій області 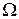, якщо 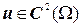і 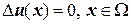., тобто функція є двічі неперервно диференційованим розв’язком рівняння Лапласа.

Означення 2 Функцію 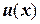називають гармонічною в деякій точці, якщо ця функція гармонічна в деякому околі цієї точки.

Означення 3 Функцію 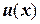називають гармонічною в деякій замкненій області, якщо вона гармонічна в деякій більш широкій відкритій області.

З гармонічними функціями у тривимірних і двовимірних областях ми вже зустрічалися, а саме нам відомо, що

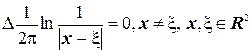(5.1)

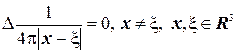(5.2)

Інтегральне представлення функцій класу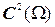

Для отримання інтегрального представлення функцій класу 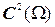будемо використовуватидругу формулу Гріна для оператора Лапласа.

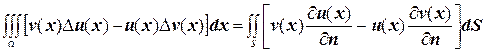(5.3)

В якості функції 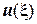оберемо довільну функцію 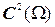, а у якості 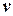, фундаментальний розв’язок оператора Лапласа для тривимірного евклідового простору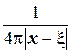

В результаті підстановки цих величин в (5.3) отримаємо

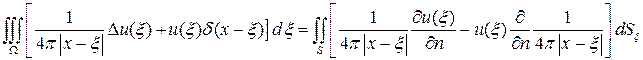Після обчислення другого доданку в лівій частині можемо записати формулу інтегрального представлення функцій класу .

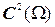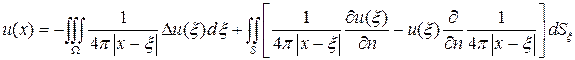(5.4)

У випадку коли функція 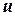є гармонічною в області 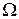то формула (5.4) прийме вигляд:

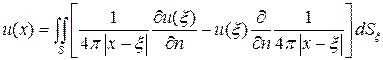(5.5)

З формули (5.5) та (5.3) можна отримати деякі властивості гармонічних функцій:

Властивість 1 Гармонічна в області 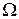функція 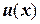має в кожній внутрішній точці області 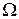неперервні похідні будь – якого порядку. Дійсно, оскільки 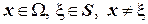, то для обчислення будь – якої похідної необхідно обчислити їх шляхом диференціювання підінтегральної функції, яка має похідні будь = якого порядку:

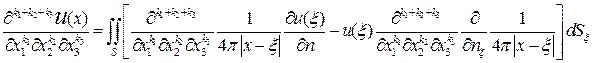
Властивість 2 Якщо 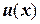гармонічна функція в скінченій області 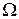с границею 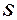то має місце співвідношення 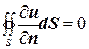(5.6)

Дійсно, у формулі (5.3) оберемо 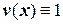. Тоді інтеграл в лівій частині і другий інтеграл правої частини перетворюється в нуль. В результаті чого отримаємо рівність (5.6).

Теорема 1 (про середнє значення гармонічної функції)

Якщо 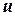функція гармонічна в кулі і неперервна в замиканні цієї кулі, то значення гармонічної функції в центрі кулі дорівнює середньому арифметичному її значень на сфері, що обмежує кулю.

Доведення Використаємо формулу (5.5) у якій в якості поверхні 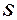візьмемо сферу радіусу 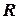з центром у точці 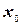, і обчислимо значення функції 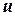в точці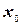

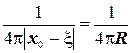Оскільки , то , а .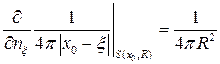

Таким чином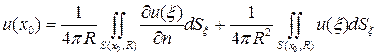

Оскільки перший інтеграл дорівнює нулю, то остаточно маємо

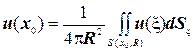(5.7)

Дата добавления: 2014-01-04