
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Макетування книжково-журнальних видань
|
|
|
|
X
X MM
Проколотий окіл – це той самий круг з якого викинули точку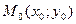 .
.
Нехай задана ф-ція двох змінних 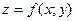 в деякому проколотому околі точки
в деякому проколотому околі точки  .
.
Число А наз. границею ф-ції 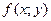 в т. (
в т. (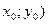 , якщо для будь-якої послідовності точок площини Оxy
, якщо для будь-якої послідовності точок площини Оxy 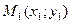 ,
, 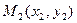 ,…,
,…,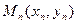 …, що лежать в проколотому околі точки
…, що лежать в проколотому околі точки 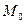 і відстань
і відстань 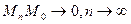 відповідні значення ф-ції
відповідні значення ф-ції 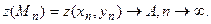
Позначення:
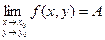
|
або 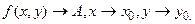
Виконується теорема: границя суми, різниці, добутку, частки двох функцій дорівнює сумі, різниці, добутку, частці їх границь (якщо це можна обчислити).
Неперервність функції
Нехай ф-ція 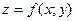 визначена в деякому проколотому околі точки
визначена в деякому проколотому околі точки  .
.
01. Якщо границя функції в точці дорівнює значенню функції в цій точці, то функція називається неперервною в точці 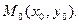
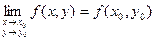
|
(1)
В точці  графік ф-ції є нерозривною поверхнею.
графік ф-ції є нерозривною поверхнею.
02. Якщо порушується умова (1), тобто границя або значення ф-ції не існують, або не рівні між собою, то точка  називається точкою розриву ф-ції
називається точкою розриву ф-ції 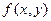 .
.
Тоді й поверхня має розриви. Ф-ція двох змінних чи поверхня може мати точки розриву і лінії розриву.
03. Ф-ція 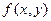 наз. неперервною в деякій області А (А – деяка площадка на площині Оху), якщо
наз. неперервною в деякій області А (А – деяка площадка на площині Оху), якщо 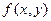 неперервна в кожній точці області А.
неперервна в кожній точці області А.
Частинні похідні і градієнт

 z
z


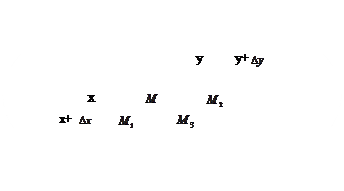 z=f(x,y)
z=f(x,y)
 z
z



 y y
y y

 | |||
 |
Нехай 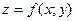 визначена в деякому околі точки М(х,у). Точка
визначена в деякому околі точки М(х,у). Точка 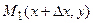 належить цьому околу.
належить цьому околу. 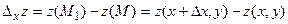 називається частковим приростом ф-ції z по змінній х в точці М.
називається частковим приростом ф-ції z по змінній х в точці М.
Аналогічно можна знайти частковий приріст ф-ції по змінній у: нехай точка 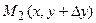 належить також області визначення функції
належить також області визначення функції  ,
,
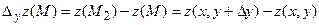
|
Якщо взяти точку 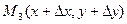 із області визначення функції, то
із області визначення функції, то
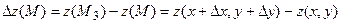
|
називається повним приростом функції z в точці М.
Означення. Частинною похідною ф-ції z в точці M(х,у) по змінній х – наз. границя відношення часткового приросту ф-ції по змінні х до приросту аргументу 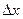 , коли , коли 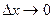 , якщо ця границя є числом. Позн. , якщо ця границя є числом. Позн. 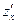 , або , або 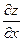 : : 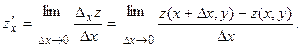
|
Аналогічно можна шукати частинну похідну по змінній у. Позн. 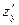 або
або 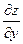 :
:
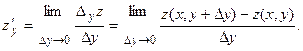
|
Оскільки означення частинної похідної по х співпадає з означенням похідної ф-ції однієї змінної х при сталому у, то частинну похідну 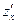 можна шукати за табличкою похідних і правилами диференціювання ф-ції однієї змінної, вважаючи х змінною, а у сталою.
можна шукати за табличкою похідних і правилами диференціювання ф-ції однієї змінної, вважаючи х змінною, а у сталою.
Аналогічно шукають 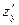 , але тоді у – змінна, а х – стала.
, але тоді у – змінна, а х – стала.
Приклад.
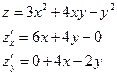
| Домашнє завдання на I практ.заняття. Повторити табличку похідних і правила диференціювання. Написати її в зошит з прак. занять. |
Нехай треба знайти частинні похідні в точці М(3;0), то
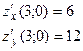 , тобто підставляють координати точки у частинні похідні.
, тобто підставляють координати точки у частинні похідні.
Отже, частинні похідні ф-ції двох змінних в точці це два числа.
Вектор з такими координатами 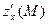 і
і 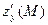 наз. повною похідною або градієнтом
наз. повною похідною або градієнтом
ф-ції z в точці М. Позн. 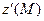 або
або 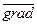
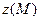
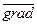 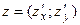
|
Пр.1. 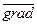
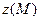
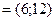
Пр.2. 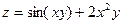 Знайти:
Знайти: 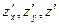 в точці М(0;1)
в точці М(0;1)
 Повний приріст функції і диференціал
Повний приріст функції і диференціал

|
 Нехай точки
Нехай точки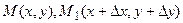 належать області
належать області
визначення функції z.
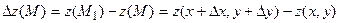
- 
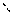 повний приріст ф-ціїв точці М(x;y).
повний приріст ф-ціїв точці М(x;y).


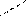

 Якщо повний приріст ф-ції в точці М
Якщо повний приріст ф-ції в точці М 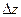 можна ось так виразити через прирости аргументів
можна ось так виразити через прирости аргументів
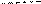  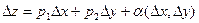
|
, де 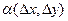 швидше прямує до нуля ніж
швидше прямує до нуля ніж
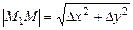 при
при 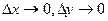 :
: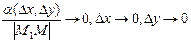 ,а
,а 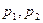 - деякі числа, то функція називається диференційованою в точці М(х,у).
- деякі числа, то функція називається диференційованою в точці М(х,у).
Величиною 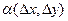 можна знехтувати.
можна знехтувати.
Основна частина приросту називається диференціалом функції і позначається dz:
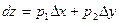
|
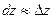
|

якщо прирости аргументів 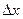 і
і 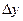 малі.
малі.
Приклад. Знайти приріст і диференціал функції 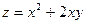 в т.М(1,-2).
в т.М(1,-2).

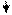
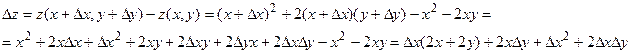
р р
р
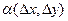 -
-
нескінченно швидше прямує до нуля ніж відстань М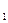 М при
М при 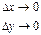
Отже, dz=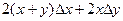 .
.
В точці М: 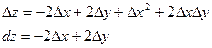
Теорема. Якщо f диференційована в точці М(х,у), то існують частинні похідні в т.М, які дорівнюють числам 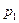 та
та 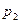 відповідно:
відповідно:
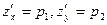
|
Тоді формула диференціалу має вигляд:
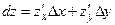
|
Перевіримо формулу на нашому прикладі
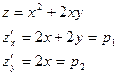
тоді 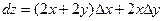 - зійшлося.
- зійшлося.
Якщо 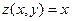 , то
, то 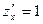 ,
, 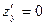 і
і 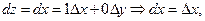
Аналогічно 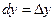 .
.
і формула для диференціалу набуває вигляду:
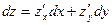
|
(1)
Ця формула диференціалу має таку властивість інваріантності: вона правильна навіть тоді, коли х та у є внутрішніми функціями від інших змінних.
Похідна складної функції
1) Якщо функція двох змінних 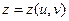 , де
, де 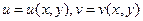 , тобто аргументи u та v є внутрішніми функціями від змінних х та у то її частинні похідні шукаються за формулами:
, тобто аргументи u та v є внутрішніми функціями від змінних х та у то її частинні похідні шукаються за формулами:
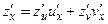
|
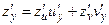
|
Mожна показати це, використовуючи властивість інваріантності диференціалу 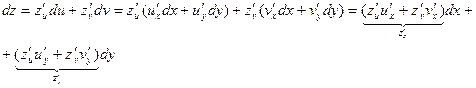
Приклад. 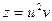 , де
, де 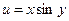 ,
, 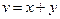
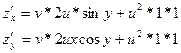

2)Якщо ф-ція  , де
, де 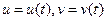 , тобто u та v є внутрішніми функціями від змінної t, тоді z є складеною функцією від одної змінної t і її похідну шукають аналогічно за формулою.
, тобто u та v є внутрішніми функціями від змінної t, тоді z є складеною функцією від одної змінної t і її похідну шукають аналогічно за формулою.
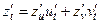
|
Приклад. 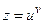 , де
, де 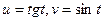
Підставивши u та v отримаємо складну ф-цію 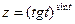 , з якої важко взяти похідну. Треба логарифмувати. А за нашою формулою
, з якої важко взяти похідну. Треба логарифмувати. А за нашою формулою
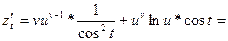 (можна тепер підставити u та v)
(можна тепер підставити u та v) 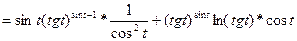 .
.
Похідна неявно заданої функції
1) Нехай функція однієї змінної y = y (x) задана неявно,
|
тобто рівнянням, де, де F – функція двох змінних.
Візьмемо диференціали з обох частин цього рівняння: dF = 0 і, оскільки, формула диференціалу правильна і тоді коли х чи у є внутрішніми функціями,
dF = Fx’ dx + Fу’ dy,
Fx’dx + Fу’dy = 0.
З цього рівняння знайдемо похідну:
 у’x =
у’x = 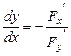 тобто в чисельнику береться похідна з F по змінній, а в знаменнику похідна з F по функції
тобто в чисельнику береться похідна з F по змінній, а в знаменнику похідна з F по функції
2) Нехай функція двох змінних z(x, y) задана неявно, тобто рівнянням
|
, де F (x, y, z) – функція трьох змінних.
Коли ми шукаємо zx’, то х – змінна, z – функція, а у – стала. Тому на
|
Аналогічно, коли ми шукаємо zy’, то у – змінна, z – функція і тоді:
|
Приклад.
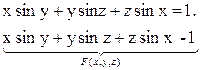
 z’x =
z’x = 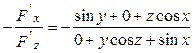
z’у = 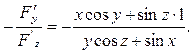
Похідна в напрямку

|


 точки М (x, y) і напрямок руху в площині
точки М (x, y) і напрямок руху в площині
Оху вектор 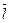 = (
= ( ). Позначимо вектор
). Позначимо вектор

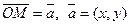




 Точка M1 така, що приріст-вектор
Точка M1 така, що приріст-вектор 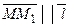 . Тоді
. Тоді 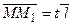 , де
, де 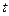 -деяке число, вектор
-деяке число, вектор 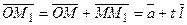 а точка M1
а точка M1
 має такі ж координати як вектор
має такі ж координати як вектор 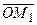
Приріст функції в напрямку 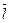 це
це
|
Приріст аргументу 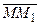 буде прямувати до нуля, якщо t → 0.
буде прямувати до нуля, якщо t → 0.
|
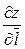 а бо
а бо 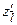 .
.
Фізичний зміст 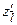 це швидкість зростання функції в даному напрямку.
це швидкість зростання функції в даному напрямку.
Частинні похідні z’x та z’y – це похідні в напрямках осей Ох та Оу відповідно, тобто в напрямках 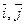 .
.
Властивість похідної в напрямку. Похідна залежить тільки від напрямку і не залежить від довжини вектора 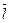 :
:
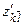 (M) =
(M) = 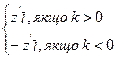
|
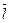 дорівнює проекції вектора-градієнта функції z в точці М на вектор
дорівнює проекції вектора-градієнта функції z в точці М на вектор 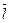 :
: 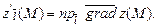
Нагадування: 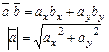
Доведення теореми. 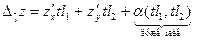 ,
,
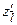 =
= 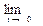
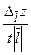 =
= 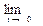
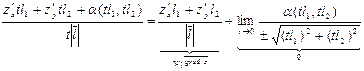 .
.
Зауваження. Проекція вектора на вектор також не залежить від довжини
вектора, на який проектують.
Приклад. z = x4 + y4 + 2x3y, 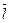 =(3,4). Знайти
=(3,4). Знайти 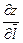 в точці M (1; 2).
в точці M (1; 2).
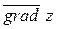
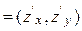
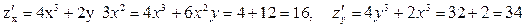
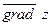 (M) = (16; 34)
(M) = (16; 34)
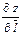 = пр
= пр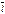
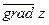 =
= 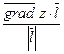 =
= 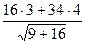 =
= 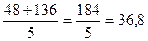 .
.
Похідні вищих порядків
Нехай задана функція двох змінних z = f (x, y).
Її частинні похідні z’x та z’y є також функціями двох змінних х, у.
З них також можна брати частинні похідні.
(z’x)’х позначається z’’xx або 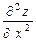 , ((z’у)’у позначається z’’xу або
, ((z’у)’у позначається z’’xу або 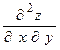 .
.
(zу)’х позначається z’’уx або 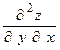 .
.
(z’у)’у позначається z’’у2 або 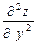 .
.
Це будуть частинні похідні другого порядку для початкової функції. Їх є чотири і їх складають у матрицю – повну похідну другого порядку:
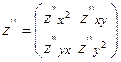 |
Приклад. z = x2 sin y. Знайти похідні другого порядку і z’’ в точці М (1;  ).
).
z‘х = 2x sin y
z’у = х2 cos y
z‘’х2 = 2 sin y = 2 sin 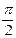 = 2
= 2
z ‘’хy = 2x cos y = 2 cos 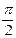 = 0
= 0 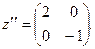
z‘’yx = 2x cos y = 2 cos 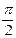 = 0
= 0
z‘’y2 = x2 (-sin y) = 1 (-sin 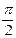 ) = - 1.
) = - 1.
Похідні z‘’yx і z‘’хy називають змішаними похідними другого порядку.
Теорема. Якщо змішані похідні z‘’yx, z‘’хy існують і неперервні в деякому околі точки М, то вони рівні: z‘’yx =z‘’хy.
(Можна переконатись в справедливості теореми на попередньому прикладі.)
Дослідження на екстремум
Означення. Точка Мо (хо, уо) називається точкою максимуму (мінімуму) функції z = f (x, y) в області D, якщо для всіх точок М (х, у) із області D
f (х, у)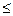 f (xo, yo) (f (х, у)
f (xo, yo) (f (х, у)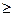 f (xo, yo)).
f (xo, yo)).
Точки максимуму і мінімуму називаються точками екстремуму. Якщо точка є екстремумом в деякому околі точки Мо то вона називається точкою локального екстремуму функції.
Теорема 1 (необхідна умова локального екстремуму). Якщо Мо (хо, уо) є точкою локального екстремуму функції f (х, у) і існують z‘х і z’у то
вони рівні нулю, тобто виконується система рівнянь:
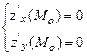
Доводиться аналогічно як для функції однієї змінної.
Теорема 2 (достатня умова локального екстремуму).
Якщо в точці Мо (хо, уо) частинні похідні І-го порядку рівні нулю: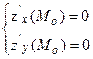 ,
,
то шукають повну похідну другого порядку матрицю z’’ (Mo) і її визначник
det z’’(Мо) і можливі три випадки:
1) det z’’ (Мо) < 0, то немає екстремуму в цій точці.
2) det z’’ (Мо) > 0, то Мо є точкою екстремуму: мінімум, якщо z‘’х2 (Мо) > 0 і максимум, якщо z‘’х2 (Мо) < 0.
3) det z’’(Мо) = 0, то екстремум може бути або не бути, потрібні додаткові дослідження.
Приклад. z = (x – 1)2 + 2y2. Дослідити на екстремум.
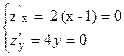 х = 1, у = 0 Мо (1, 0) – критична точка.
х = 1, у = 0 Мо (1, 0) – критична точка.
z‘’х2 = 2
z‘’хy = 2
z‘’хy = 0
z‘’хy = 0 z’’ = 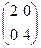
z‘’у2 = 4 det z’’ = 8 – 0 = 8 > 0. Отже, є екстремум в точці (1; 0).
z‘’х2 = 2 > 0, тобто є min, zmin = z (1; 0) = 0 + 0= 0.




 Дослідження функції двох змінних на найбільше і найменше значення в закритій області
Дослідження функції двох змінних на найбільше і найменше значення в закритій області
а) Шукають критичні точки, які входять в область і, в яких z‘х і z’у дорівнюють нулю або не існують.
 б) Шукають критичні точки на межі області. Якщо треба, розбивають її на
б) Шукають критичні точки на межі області. Якщо треба, розбивають її на
різні криві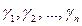 . На кожній кривій функція z стає функцією однієї змінної (якщо з рівняння кривої виразити одну змінну через іншу і підставити знайдений вираз у формулу функції z).
. На кожній кривій функція z стає функцією однієї змінної (якщо з рівняння кривої виразити одну змінну через іншу і підставити знайдений вираз у формулу функції z).
в) Обчислюють значення функції z в усіх знайдених критичних точках і в точках, де з’єднуються криві 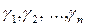 і вибирають з них найбільше та найменше значення.
і вибирають з них найбільше та найменше значення.
Приклад. Знайти найбільше і найменше значення функції z = x2 + y2 - xy +x+ y в області D, обмеженій лініями x=0, y=0, x+y+3=0.
Зобразимо область D. Це трикутник у третій координатній чверті.
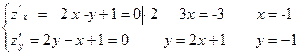 М(-1;-1) є D.
М(-1;-1) є D.
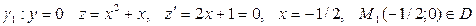 ,
,

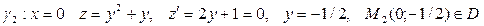 ,
,
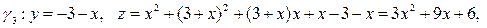
|

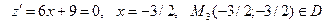 .
.



 Добавимо ще точки А(-3;0), В(0;0), С(0;-3).
Добавимо ще точки А(-3;0), В(0;0), С(0;-3).
 z(M)=z(-1;-1)=1+1-1-1-1=-1 -- найменше значення z
z(M)=z(-1;-1)=1+1-1-1-1=-1 -- найменше значення z
z(M1)=z(-1/2;0)=1/4-1/2=-1/4 z(M2)=-1/4
z(M3)=9/4+9/4-9/4-3/2-3/2=-3/4
z(A)=z(C)=z(-3;0)=9-3=6 -- найбільше значення z
z(B)=z(0;0)=0.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 553; Нарушение авторских прав?; Мы поможем в написании вашей работы!
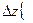 z(M)
y y+
z(M)
y y+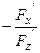
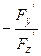
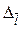 z
z  z=f(x,y)
z(M)
O
z=f(x,y)
z(M)
O
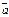 M
M
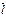
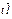 M1
M1
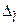 z= z (M1) –z (M) = z (
z= z (M1) –z (M) = z (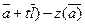
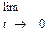
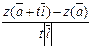
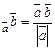
 M1 B
M2
M
M3
M1 B
M2
M
M3 
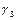 -3
C
-3
C