Нормальные колебания многоатомной молекулы и нормальные колебательные координаты

Нормальные колебания многоатомной молекулы – это колебания гармонических осцилляторов, т.е. колебания в отсутствие затухания энергии.

Колебательная энергия совокупности гармонических осцилляторов описывается выражением

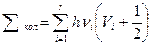, (2.32)

где 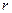- число колебательных степеней свободы; 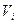- колебательное квантовое число 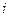-го осциллятора; - частота 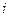-го нормального колебания.

Число нормальных колебаний (число полос в колебательном спектре) определяется:

а) количеством атомов 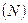в молекуле; б) симметрией молекулы.

в)смещением каждого атома в молекуле в напралении трёх координатных осей .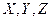

Следовательно, для молекулы из 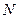атомов возможны 3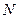смещений атомов. Если из 3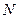степеней свободы движений атомов исключить движения, при которых взаимное положение атомов в молекуле не меняется (это - три компоненты поступательного движения молекулы, как целого и три компоненты вращательного движения молекулы, как целого), то получим следующие формулы для определения количества нормальных колебаний :

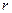для линейных молекул 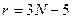, для объемных .

По характеру движения атомов в молекуле друг относительно друга нормальные колебания подразделяются: на валентные -симметричные и ассимметричные (определяются периодическими смещениями атомов по линиям связи) и деформационные-симметричные и ассимметричные (определяются изменением угла между связями). Деформационные колебания подразделяются на: поперечные 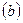, маятниковые 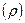, веерные 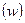, крутильные .

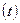Для 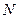атомной молекулы, не имеющей замкнутых колец, число валентных колебаний всегда равно числу связей, т.е., 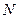-1, остальные 2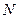-5 колебаний являются деформационными

Нормальные колебательные координаты 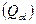: связаны с декартовыми компонентами малых смещений ядер из положений равновесия 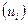унитарным преобразованием

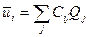, (2.33)

,

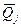
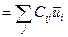где - унитарная матрица; .

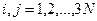Энергия системы частиц, совершающих малые колебания в декартовых координатах записывается формулой

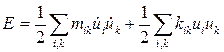, (2.34)

где m_ik, k_im = const.

В нормальных координатах выражение (2.34) имеет вид:

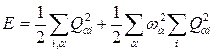, (2.35)

где w_a – соответствующие частоты колебаний; a – нумерует частоты; i = 1, 2, …, f_a – нумерует координаты, относящиеся к одной a-й частоте (f_a – кратность частоты).

Выражение (2.35) для энергии молекулы должно быть инвариантным по отношению к преобразованиям симметрии. При всяком преобразовании нормальные координаты Q_ai преобразуются линейно друг через друга, так, что сумма 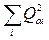остается неизменной.

Другими словами осуществляют некоторое неприводимое представление ее группы симметрии. Кратность вырождения частоты определяет размерность этого представления. Эти соображения дают возможность произвести классификацию собственных колебаний молекулы. Для этого сначала находится полное колебательное представлении

2.12 Полное колебательное представление

Это приводимое представление, осуществляемое сразу всеми колебательными координатами. Разложением его на неприводимые части определяется кратность вырождения собственных частот и симметрия соответствующих колебаний.

Для этого используются не нормальные координаты Q_ai, а компоненты (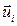) векторов смещения ядер из их положения равновесия. При вычислении характеров рассматриваются только те ядра, положения равновесия которых при данном преобразовании симметрии остаются на месте.

Действительно, если при повороте или отражении ядро 1 перемещается в новое положение, где до этого находилось другое такое же ядро 2, это значит, что при данной операции симметрии в соответствующих этому ядру строках матрицы G_ik не будет диагональных элементов (нет вклада в характер). Компоненты же вектора смещения ядра, положение равновесия которого не затрагивается операцией симметрии G, преобразуются только друг через друга. Их можно рассматривать независимо от векторов смещения остальных ядер.

Пример 2.11:Определить характер матрицы поворота C(j) на угол j вокруг оси z.

Алгоритм решения: пусть u_x, u_y, u_z – компоненты вектора смещения некоторого ядра, положение равновесия которого находится на самой оси. При повороте эти компоненты преобразуются, как компоненты обычного (полярного) вектора по формулам

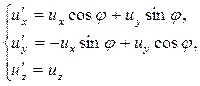; (2.36)

Здесь u'_i – новые компоненты вектора после поворота системы координат против часовой стрелки.

Характер (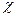)- сумма диагональных элементов матрицы преобразования, равен 1+2cosj. Если на оси находится N_c ядер, то суммарный характер равен

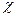=N_c(1+2 cos j). (2.37)

В (2.37) необходимо отделить части, соответствующие поступательному перемещению молекулы, как целого - характер 1+2cosj и вращательному движению молекулы, как целого - характер 1- 2cosj._

В результате будем иметь формулы:

для поворота C(j)

; (2.38)

для единичного элемента при N_c=N, j=0

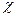(E)=3N-6.;

Дата добавления: 2014-01-04