Для зеркально-поворотного преобразования получим

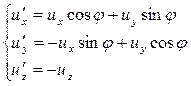, (2.39)

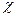
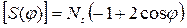,. (2.40)

вклады в характер от поступательного движения (-1+2cosj) и от вращения молекулы, как целого (1-2cosj)) компенсируются..

характеры для плоскости симметрии (при j=0),; и для инверсного элемента (при j=p):

определяются по формулам

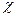(s)=N_s;

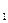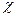(I) = -3N_I.,

соответственно

Таким образом, используя приведенные формулы, определяются характеры 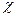(G) полного колебательного представления.

1) Используя формулу (2.5) полное колебательное представление разлагается на неприводимые части, затем производится классификация нормальных колебаний молекулы.согласно таблицы характеров соответствующих точечных групп (табл.2 приложение 1)

Пример 12. Провести классификацию внутренних коле- баний молекулы NH₃ (рис. 2.8), точечная группа симметрии C_3v.

_{Алгоритм решения:: приводятся структура и элементы симметрии рассматриваемой системы; из таблиц характеров (табл.2,Приложение 1); выписываются представления точечной группы симметрии} C_3v. и сводятся в таблицу(табл.2.7)

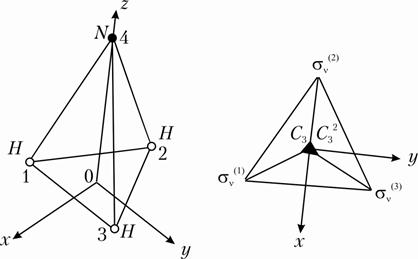
а) б)

Рис. 2.8. а – структура молекулы NH₃; б – проекция элементов симметрии C_3v молекулы на плоскость на ХОY.

_:

Табл. 2.7. Представления точечной

группы симметрии C_3v.

C3v	E	2C­3	3sv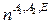
A1; z
A2			-1
E; x, y		-1
c(G)

Пользуясь нижеприведенными формулами вычисляются характеры полного колебательного представления c (G):

c(E) = 3N-6 = 3×4-6 = 6;

, (один атом азота на оси);

c(s_V)=N_s=2,

(на плоскости лежат один атом азота N и один водорода Н).

Полученные результаты записываются в соответствующие столбцы табл. 2.7 для каждого класса элементов симметрии. Характеры элементов одного класса, как известно, одинаковы.

Используя формулу разложения приводимого представления на неприводимые, выраженную через характеры

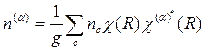, (2.41)

где n_c – число элементов в классе; 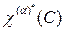– характер элемента неприводимого a-представления,

полное колебательное представление c(G) разлагается по неприводимым представлениям группы C_3V следующим образом:

; ; ,

.

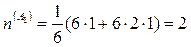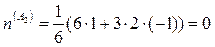Полученные данные записываются в соответствующие строки табл. 2.7.

Из результатов разложения заключаем, что спектр внутримолекулярных колебаний молекулы NH₃ состоит из четырех частотных полос: две полосы– невырожденные, они характеризуют полносимметричные колебания(2A₁); две полосы (2Е) – характеризуют двукратно вырожденные колебания симметрии (2Е). Активность колебаний в инфракрасных спектрах (ИКС) поглощения и спектрах комбинационного рассеяния (КРС) света определяется из таблицы характеров точечных групп (табл.2 Приложение 1).

Пример2.13Произвести классификацию внутримолекулярных колебаний структурной группы [T_iO₆] (рис. 2.9) в титанате бария (BaTiO₃), точечная группа симметрии O_h (табл. 2.8).

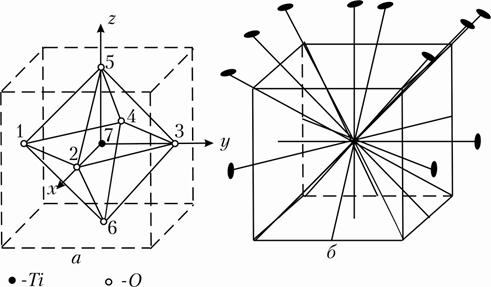
Рис. 2.9. Структура [T_iO₆] (а) и элементы симметрии группы O_h в кубе (б): 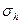- координатные плоскости; 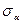- диагональные плоскости, включающие ось 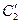и противоположные ребра

Алгоритм решения: приводятся соответствующие. структурная группа (рис. 2.9 –а) и элементы симметрии точечной группы (рис.29 –б) и приводятся её неприводимые представления точечной группы симметрии (табл. 2.8)

Табл. 2.8.Неприводимые представления точечной группы симметрии O_h.

Oh	E	8C3	3C2	6C4	C'2	I	8S6	3sh	6S4	6sd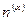
A1g
A2g				-1	-1				-1	-1
Eg		-1					-1
F1g			-1		-1			-1		-1
F2g			-1	-1				-1	-1
A1u						-1	-1	-1	-1	-1
A2u				-1	-1	-1	-1	-1
Eu		-1				-2		-2
F1u			-1		-1	-3			-1
F2u			-1	-1		-3				-1
c(G)			-1			-3			-1

По формулам (2.37 -2.40) вычисляем характеры полного колебательного представления c(G). структурной группы [T_iO₆

Получаем: 1) c(E)=3N-6=3×7-6=15; 2) c(C₃)=0, так как 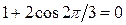; 3) c(C₂=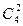)=(3-2)(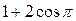)=-1, на осях 3C₂ (координатные оси) лежат три атома - один титана и два кислорода; 4) c(C₄)=(3-2)(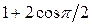) = 1; 5) c(C'₂)=(1-2)(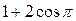)=1, оси 6C'₂ проходят через центр куба и середины противоположных ребер; 6) c(I)=-3N_I­­=-3; 7)c(S₆)=1×(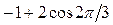) = 0; оси S₆ – это пространственные диагонали куба; 8) c(s_h)=5; 9) c(S₄)=1×(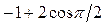)= = -1, оси S₄ – координатные оси; 10) c(s_d) = 3. Результаты вычислений сводятся в нижнюю строку табл. 2.8

Разлагая характер полного колебательного представления c(G) по неприводимым представлениям группы O_h. с помощью формулы (2.5), получаем:

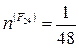[15×3+3×(-1)×(-1)+6×(-1)×1+6×1×1+(-3)×(-3)+

+3×5×1+6×(-1)×1+6×3×(-1)]=1;

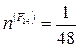[15×3+3×(-1)×(-1)+6×1×1+6×1×(-1)+(-3)×(-3)+

+3×5×1+6×(-1)×(-1)+6×3×1]=2 и т. д.

Производя вычисления для всех неприводимых представлений группы O_h, будем иметь

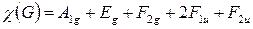. (2.42)

Правильность вычислений проверяется следующим образом: размерность матрицы, по которой преобразуются все внутримолекулярные колебания (ее характер c(G)), равна 3N-6=15. должна быть равна размерности правой части выражения (2.42) и если она будет равна 15, то вычисление проведено правильно. Суммируем 1´1+1´2+1´3+2´3+1´3=15, т. е. все неприводимые части c(G) найдены.

Таким образом, спектр внутримолекулярных колебаний структурной единицы [TiO₆] в кубическом BaTiO₃ состоит из шести частотных полос, из них:

A_1g – полносимметричное, невырожденное колебание;

E_g – двукратно вырожденное;

F_2g, F_1u, F_2u, – трехкратно вырожденные.

Индексы g, u показывают симметричное (g) или несимметричное (u) относительно операции инверсии колебание. Относительно определения активности колебаний следует обратиться к таблице характеров группы O_h (табл.2 Приложение1).

На практике спектр может иметь большее количество частотных полос, чем это следует из разложения типа (2.42).

В экспериментальных спектрах возможно частичное (или полное) снятие вырождения колебаний из-за понижения симметрии вследствие ангармонизма или структурных искажений. Это можно показать на примере колебательных спектров оксианионов

Дата добавления: 2014-01-04