
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Розподіли Бозе-Ейнштейна та Фермі-Дірака
|
|
|
|
Розподіл Больцмана. Барометрична формула
Розподіл Максвела. Характеристичні швидкості молекул
Лекція №5 Статистичні розподіли
ü Розподіл Максвела. Характерні швидкості молекул
Згідно до основних постулатів молекулярно-кінетичної теорії (МКТ) газів, молекули перебувають в безупинному, хаотичному русі. Природно виникає запитання про розподіл молекул за швидкостями. Із загальних міркувань зрозуміло, що швидкості молекул є різними, і до того ж вони часто і помітно змінюються в часі, зокрема, після зіткнень молекул поміж собою, або зі стінками тої ємності, в якій вони перебувають. Найбільша доля молекул мають швидкості навколо деякої середньої величини, тоді як молекул з дуже великими, або дуже малими (відносно середньої) швидкостями є порівняно небагато.
З огляду на величезну кількість молекул в газі неможливо прослідкувати за кожною з них. На практиці цікавляться питанням: яка доля молекул (відсоток молекул) має швидкості в тому чи іншому інтервалі швидкостей. Варто одразу визначитися, що ми цікавитимемося лише модулем швидкості молекул, тому що напрям вектора швидкості молекули є абсолютно випадковим, тобто в кожному можливому напрямі рухається однакова відносна кількість молекул.
Отже, модуль швидкості пересічної молекули лежить в межах від  до
до  : тобто
: тобто  . Насправді безкінечних швидкостей в природі не може бути, тому права межа у наведеній нерівності є лише певним наближенням. (Можливо, краще було б написати
. Насправді безкінечних швидкостей в природі не може бути, тому права межа у наведеній нерівності є лише певним наближенням. (Можливо, краще було б написати 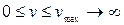 ).
).
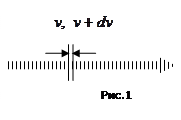 Розділимо вказаний інтервал швидкостей на рівні проміжки шириною
Розділимо вказаний інтервал швидкостей на рівні проміжки шириною  . Ліва межа такого проміжку шириною
. Ліва межа такого проміжку шириною  відповідає деякій швидкості
відповідає деякій швидкості  , тоді як права межа – швидкості
, тоді як права межа – швидкості  . Визначимо, яка частина молекул (
. Визначимо, яка частина молекул ( ) газу має швидкості в інтервалі від
) газу має швидкості в інтервалі від  до
до  ?
?
Ця величина є різною для різних інтервалів показаних на рис.1, але вона повинна бути пропорційною ширині проміжку  . Іншими словами, треба припускати, що існує пряма пропорційність поміж величинами
. Іншими словами, треба припускати, що існує пряма пропорційність поміж величинами  та
та  , причому коефіцієнт пропорційності
, причому коефіцієнт пропорційності  залежить від швидкості
залежить від швидкості  :
:

| (1) |
Коефіцієнт пропорційності, позначений в (1) як  , має назву функції розподілу Максвела, бо першим вигляд цієї функції знайшов англійський фізик Джеймс Клерк Максвел.
, має назву функції розподілу Максвела, бо першим вигляд цієї функції знайшов англійський фізик Джеймс Клерк Максвел.
Функція Максвела (або розподіл Максвела) має наступний вигляд:
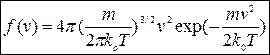
| (2) |
 де
де 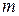 - маса молекули,
- маса молекули,  - абсолютна температура газу, а
- абсолютна температура газу, а  - стала Больцмана. Функція (2) має типовий дзвіноподібний вигляд з одним максимумом, як це показано на рис.2.(по осі ординат відкладена функція Максвела, по горизонтальній осі відношення швидкості молекули до найбільш ймовірної швидкості молекули -
- стала Больцмана. Функція (2) має типовий дзвіноподібний вигляд з одним максимумом, як це показано на рис.2.(по осі ординат відкладена функція Максвела, по горизонтальній осі відношення швидкості молекули до найбільш ймовірної швидкості молекули -  ).
).
На рис.2 показані функції Максвела для трьох різних температур газу. Зі збільшенням температури криві стають нижчими у максимумі, ширшими, а положення максимуму функції  зміщується у бік більших швидкостей. Положення цього максимуму неважко знайти, якщо диференціювати функцію (2) по швидкості і похідну прирівняти нулю:
зміщується у бік більших швидкостей. Положення цього максимуму неважко знайти, якщо диференціювати функцію (2) по швидкості і похідну прирівняти нулю:

| (3) |
Рішенням рівняння (3) є швидкість:
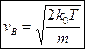
| (4) |
Швидкість (4) визначає найбільш ймовірну швидкість молекул газу, або таку швидкість, на яку припадає максимум функції Максвела  . Напевно, що кінетична енергія, яка відповідає швидкості (4), задовольняє умові:
. Напевно, що кінетична енергія, яка відповідає швидкості (4), задовольняє умові:

| (5) |
Отже, температура характеризує кінетичну енергію молекул, проте коефіцієнт зв’язку поміж найбільш ймовірною кінетичною енергією молекули та величиною  , який дорівнює
, який дорівнює  у формулі (5) відрізняється від коефіцієнта
у формулі (5) відрізняється від коефіцієнта  , введеного раніше під час визначення температури як міри середньої кінетичної енергії молекули.
, введеного раніше під час визначення температури як міри середньої кінетичної енергії молекули.
Отже, найбільш ймовірна кінетична енергія молекули, яка фігурує в лівій частині (5) є трохи меншою від середньої кінетичної енергії молекул:

| (6) |
Окрім того, крива розподілу Максвела не є симетричною, тому частина молекул, яка задовольняє умові  є меншою від 50%. Середньоквадратична, швидкість
є меншою від 50%. Середньоквадратична, швидкість  відповідає умові, яка є наслідком рівняння (6):
відповідає умові, яка є наслідком рівняння (6):

| (7) |
Середню швидкість молекули (математичне очікування) можна знайти згідно загального правила для нормованої функції  :
:

 (8)
(8)
Співставлення виразів (4,7,8) дає
 (9)
(9)
Рис.2 ілюструє це співвідношення.
 Експериментальне визначення швидкостей молекул можливе на устаткуванні, схема якого показана на рис.4. „Молекулярна гармата” (джерело молекул) та система діафрагм формує вузький пучок (промінь) молекул, які проходять крізь зміщені прорізи у двох дисках, котрі обертаються з однаковою частотою
Експериментальне визначення швидкостей молекул можливе на устаткуванні, схема якого показана на рис.4. „Молекулярна гармата” (джерело молекул) та система діафрагм формує вузький пучок (промінь) молекул, які проходять крізь зміщені прорізи у двох дисках, котрі обертаються з однаковою частотою  . Молекула, яка пройшла крізь проріз у першому дискові потрапить на детектор лише при виконанні умови, що за час її прольоту
. Молекула, яка пройшла крізь проріз у першому дискові потрапить на детектор лише при виконанні умови, що за час її прольоту  поміж дисками кут повороту другого диску складе фіксовану величину
поміж дисками кут повороту другого диску складе фіксовану величину  . Отже швидкість молекули
. Отже швидкість молекули  , відстань поміж дисками
, відстань поміж дисками 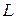 , частота обертання, та кут зміщення прорізів
, частота обертання, та кут зміщення прорізів  , повинні задовольняти рівнянню:
, повинні задовольняти рівнянню:

| (10а) |
звідки швидкість молекули, яка потрапила у детектор дорівнює:

| (10б) |
Змінюючи частоту обертання дисків  , можна пропускати на детектор молекули різної швидкості, як це видно з (10б) і таким шляхом експериментально перевірити розподіл Максвела.
, можна пропускати на детектор молекули різної швидкості, як це видно з (10б) і таким шляхом експериментально перевірити розподіл Максвела.
ü Розподіл Больцмана, барометрична формула
 Розподіл Больцмана описує поведінку молекул ідеального газу в зовнішніх потенціальних силових полях.
Розподіл Больцмана описує поведінку молекул ідеального газу в зовнішніх потенціальних силових полях.
Припустимо, що газ знаходиться в такому силовому полі з потенційною енергією, яка залежить від координат:  . Тоді як статистична теорія, так і експеримент показують, що концентрація молекул більша в тих місцях, де потенційна енергія поля є меншою, і навпаки, концентрація молекул є малою там, де потенційна енергія поля зростає (це твердження ілюструє рис.5, який моделює розподіл частинок у полі сил тяжіння).
. Тоді як статистична теорія, так і експеримент показують, що концентрація молекул більша в тих місцях, де потенційна енергія поля є меншою, і навпаки, концентрація молекул є малою там, де потенційна енергія поля зростає (це твердження ілюструє рис.5, який моделює розподіл частинок у полі сил тяжіння).
Математично ця закономірність віддзеркалюється розподілом Больцмана для концентрації молекул:

| (11) |
де  - концентрація молекул там, де
- концентрація молекул там, де 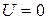 .
.
Зокрема в полі тяжіння Землі, потенційна енергія якого залежить від висоти над поверхнею моря по закону 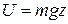 , розподіл молекул по висоті такий, що концентрація молекул, тиск та густина повітря з висотою падають згідно з барометричною формулою:
, розподіл молекул по висоті такий, що концентрація молекул, тиск та густина повітря з висотою падають згідно з барометричною формулою:
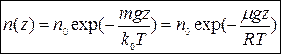
| (12) |
 З формули (12) слідує, що із зниженням температури концентрація частинок на висоті
З формули (12) слідує, що із зниженням температури концентрація частинок на висоті 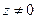 убуває, обертаючись у нуль при
убуває, обертаючись у нуль при  (рис.6). При абсолютному нулі усі молекули розташувалися б на земній поверхні. При високих температурах, навпаки,
(рис.6). При абсолютному нулі усі молекули розташувалися б на земній поверхні. При високих температурах, навпаки, 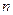 слабко убуває з висотою, таким чином, що молекули розташовуються з висотою майже рівномірно. Такий розподіл молекул у поля тяжіння Землі можна якісно, у межах молекулярно-кінетичних уявлень, пояснити тим, що на молекули впливає два протилежних фактори: гравітаційне поле, під дією якого всі молекули притягуються до Землі, і молекулярний хаотичний рух, який намагається рівномірно розкидати молекули по усьому можливому об’єму.
слабко убуває з висотою, таким чином, що молекули розташовуються з висотою майже рівномірно. Такий розподіл молекул у поля тяжіння Землі можна якісно, у межах молекулярно-кінетичних уявлень, пояснити тим, що на молекули впливає два протилежних фактори: гравітаційне поле, під дією якого всі молекули притягуються до Землі, і молекулярний хаотичний рух, який намагається рівномірно розкидати молекули по усьому можливому об’єму.
Больцман довів, що розподіл (12) є справедливий не тільки у випадку потенційного поля сил земного тяжіння, але і у будь-якому потенційному полі сил для сукупності будь-яких однакових частинок, які знаходяться у стані хаотичного теплового руху.
Якщо обидві частини (12) помножити на  і припустити, що температура мало змінюється з висотою
і припустити, що температура мало змінюється з висотою 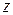 (що дещо сумнівно, особливо для великих висот), можна отримати вираз для тиску, як функції висоти над рівнем моря:
(що дещо сумнівно, особливо для великих висот), можна отримати вираз для тиску, як функції висоти над рівнем моря:

| (13) |
Вимірюючи тиск барометром, за барометричною формулою (13) можна розрахувати висоту над рівнем моря (так, наприклад, діють авіаційні альтиметри - сенсори висоти).
ü Розподіли Бозе-Ейнштейна та Фермі-Дірака
Всі квантові частинки поділяють на два класи. Одним з цих двох класів є так звані бозони, іншим класом є ферміони.
Відносно ферміонів в квантовій механіці доводиться принцип заборони Паулі, який стверджує, що в будь-якому квантовому стані 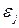 може знаходитися не більше ніж один ферміон. Таким чином, кожний квантовий стан
може знаходитися не більше ніж один ферміон. Таким чином, кожний квантовий стан 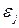 в системі ферміонів або зайнятий, і то лише одним ферміоном (
в системі ферміонів або зайнятий, і то лише одним ферміоном ( ), або вільний (
), або вільний ( )
)
Для бозонів ситуація є протилежною: в будь-якому квантовому стані може знаходитися як завгодно багато бозонів. Більше того, при низьких температурах більшість бозонів знаходиться в одному і тому ж квантовому стані з мінімальною енергією  , який називають основним станом системи. Чим нижче стає температура, тим більшою є кількість бозонів (
, який називають основним станом системи. Чим нижче стає температура, тим більшою є кількість бозонів ( ), скупчених в основному стані. Це явище отримало назву низькотемпературної конденсації бозонів.
), скупчених в основному стані. Це явище отримало назву низькотемпературної конденсації бозонів.
У квантовій статистичній фізиці бозони (фотони, тобто кванти електромагнітного поля; або ядерні альфа-частинки; або електронно-діркові пари, так звані екситони, у напівпровідниках; тощо) та ферміони (протони, нейтрони, електрони, тощо) по різному розподілені по енергіях.
Кажуть, що бозони підкоряються розподілу Бозе-Ейнштейна, за яким у системі бозонів середня кількість частинок  , які перебувають при температурі
, які перебувають при температурі  у стані з енергією
у стані з енергією  визначаються наступною формулою:
визначаються наступною формулою:

| (14) |
при додатковій умові, що

| (15) |
 З умови (15) випливає, що
З умови (15) випливає, що  . Інакше кажучи величина
. Інакше кажучи величина  , яку в статистичній фізиці називають хімічним потенціалом, за фізичним змістом є мінімальною енергією, яку може мати системний бозон. Інакше кажучи, для бозонів хімічний потенціал є просто енергією їх основного стану, отже,
, яку в статистичній фізиці називають хімічним потенціалом, за фізичним змістом є мінімальною енергією, яку може мати системний бозон. Інакше кажучи, для бозонів хімічний потенціал є просто енергією їх основного стану, отже,  . Умова (15) необхідна для того, щоб ліва частина (14) завжди лишалася позитивною. Неважко побачити, що при умові
. Умова (15) необхідна для того, щоб ліва частина (14) завжди лишалася позитивною. Неважко побачити, що при умові  маємо,
маємо,  , що віддзеркалює можливості згаданої низькотемпературної конденсації бозонів. Графічно залежність (14) від енергії для різних температур зображена на рис.7. Звідти видно:
, що віддзеркалює можливості згаданої низькотемпературної конденсації бозонів. Графічно залежність (14) від енергії для різних температур зображена на рис.7. Звідти видно:
- Кількість бозонів в певному енергетичному стані тим більша, чим ближчий цей стан до основного стану з енергію
 ;
; - Розподіл Бозе-Ейнштейна при нульовій температурі вироджується у вертикальну лінію при
 (
(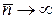 ) та горизонтальну лінію при інших енергіях
) та горизонтальну лінію при інших енергіях  (
( );
); - З ростом температури розподіл Бозе-Ейнштейна все більше відрізняються від розподілу при
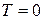 , бозони інтенсивніше „випаровуються” з основного стану (з „конденсату”) в інші енергетичні стани, де їх кількість поступово збільшується з ростом температури.
, бозони інтенсивніше „випаровуються” з основного стану (з „конденсату”) в інші енергетичні стани, де їх кількість поступово збільшується з ростом температури.
Ферміони підкоряються розподілу Фермі-Дірака:

| (16) |
Принцип заборони Паулі призводить до того, що  . Отже величину (16) можна трактувати також як ймовірність того що при температурі
. Отже величину (16) можна трактувати також як ймовірність того що при температурі  енергетичний рівень
енергетичний рівень  зайнятий ферміоном.
зайнятий ферміоном.
Хімічний потенціал  для ферміонів має зовсім інший фізичний зміст, ніж для бозонів. Якщо підставимо
для ферміонів має зовсім інший фізичний зміст, ніж для бозонів. Якщо підставимо  , то отримаємо
, то отримаємо 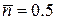 . Таким чином хімічний потенціал для ферміонів, це такий гіпотетичний енергетичний рівень, ймовірність заповнення якого точно дорівнює 0.5. Зрозуміло, що енергетичні рівні, енергія яких менша
. Таким чином хімічний потенціал для ферміонів, це такий гіпотетичний енергетичний рівень, ймовірність заповнення якого точно дорівнює 0.5. Зрозуміло, що енергетичні рівні, енергія яких менша  (тобто
(тобто 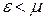 ), ймовірність заповнення більша 0.5, а для рівнів
), ймовірність заповнення більша 0.5, а для рівнів  , навпаки, менша від 0.5.
, навпаки, менша від 0.5.
При нульовій температурі  якщо
якщо 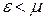 і
і  , якщо
, якщо  . Отже, при нульовій температурі хімічний потенціал
. Отже, при нульовій температурі хімічний потенціал  (який ще називають енергією Фермі) розділяє заповнені стани від незаповнених і розподіл Фермі вироджується у „сходинку Фермі” (рис.8а).
(який ще називають енергією Фермі) розділяє заповнені стани від незаповнених і розподіл Фермі вироджується у „сходинку Фермі” (рис.8а).
 Енергія Фермі (
Енергія Фермі ( ) для ферміонів і при ненульових температурах є певною межею між переважно заповненими (
) для ферміонів і при ненульових температурах є певною межею між переважно заповненими (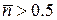 ) та переважно незаповненими (
) та переважно незаповненими ( )енергетичними станами. Втім розподіл Фермі (16) при
)енергетичними станами. Втім розподіл Фермі (16) при  дещо розмивається, як це видно з рис.8б. Причому чим більша температура, тим більше „розмиття сходинки Фермі”.
дещо розмивається, як це видно з рис.8б. Причому чим більша температура, тим більше „розмиття сходинки Фермі”.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 2183; Нарушение авторских прав?; Мы поможем в написании вашей работы!