Косий згин. Визначення нормальних напружень

У п. 3.1 ми розглядали прямий згин балок, при якому силова площина П проходить через одну з головних центральних осей її поперечного перерізу. Якщо ж силова площина П не збігається ні з однією з головних центральних осей поперечного перерізу балки, то такий згин називають косим (рис. 8.1).

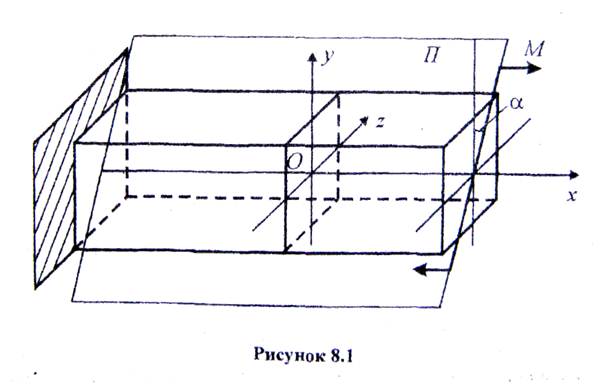
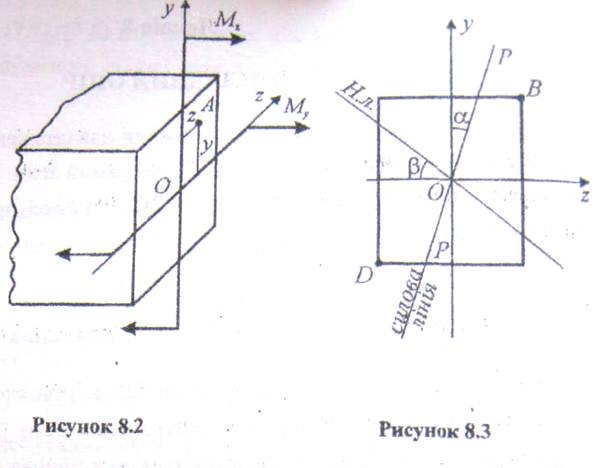
Визначимо нормальні напруження в деякій точці А(z, у) довільного попе­речного перерізу (рис. 8.2). Головні центральні осі z, у в цьому перерізі вибе­ремо так, щоб область розтягу була в 1-й чверті. Згинальний момент М в да­ному перерізі розкладаємо на складові 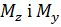де

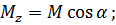
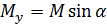(8.1).

Користуючись принципом незалежності дії сил, зведемо косий згин до двох прямих згинів у двох взаємно перпендикулярних площинах. Напруження у точці А знаходиться згідно з принципом суперпозиції як алгебраїчну суму напружень від моментів М_z і М_у. За формулою (3.16)

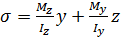(8.2)

У (8.2) моменти 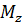і М_у беруться по модулю, а координати точки, для якої визначаються напруження, підставляються з врахуванням знаків.

8.2 Розрахунок на міцність при косому згині

Для визначення небезпечних точок у даному перерізі треба знайти поло­ження нейтральної лінії. Її рівняння визначається з умови 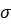(z, у)= 0, тобто

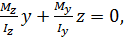(8.3)

звідки

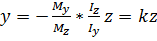(8.4)

Кут нахилу 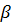нейтральної лінії до осі z знаходиться з виразу для кутового коефіцієнта k прямої (8.4)

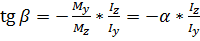(8.5)

З (8.5) видно, що на відміну від прямого згину при косому згині нейтраль­на лінія (нл.) і силова лінія (р.р.) в загальному випадку (коли 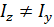) не будуть взаємно перпендикулярні (рис. 8.3). Для перевірки на міцність слід спочатку побудувати епюри згинальних моментів М_z і М_у. З цих епюр вибрати небез­печний переріз, де М_z і М_у по модулю одночасно великі. Таких перерізів мо­же бути декілька. Далі в небезпечному перерізі слід знайти небезпечні точки — це точки, які найбільш віддалені від нейтральної лінії — точки В і D (рис. 8.3). У точці В діє найбільше розтягуюче, а в точці D — найбільше стискаюче на­пруження. Умова міцності для небезпечних точок має вид

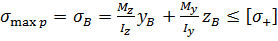
(8.6)

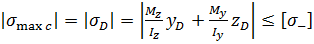
Відмітимо, що якщо поперечний переріз балки має дві осі симетрії (напри­клад, прямокутник, двотавр), то небезпечними будуть завжди кутові точки В і D (рис. 8.3). Умова міцності записується у вигляді

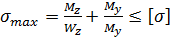(8.7) (8.7)

Для визначення прогину також використовуємо принцип незалежності дії сил і обчислюємо прогин в кожній з головних площин.

Позначимо прогин в на­прямку осі у через 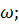а в напрямку осі г через V. Тоді диференціальні рівнян­ня прогинів у площинах хz і уz запишуться у вигляді

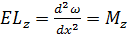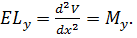; (8.8)

Інтегруючи (8.8), визначаємо О) і V.

Величина повного прогину 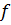перерізу визначається як геометрична сума прогинів 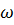і V:

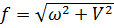(8.9)

Дата добавления: 2014-01-04