Визначення нормальних напружень

Поза центровий розтяг або стиск стержня.

Позацентровий розтяг або стиск викликається навантаженням, рівнодійна якого Р проходить паралельно до осі стержня з ексцентриситетом е.

Нехай на стержень довільного перерізу діє одна сила Р, яка паралельна до осі стержня і перетинає будь-який поперечний переріз у точці р (рис. 8.4). Ко­ординати точки р в системі головних центральних осей позначимо z_р і y_p. В будь-якому поперечному перерізі внутрішній силові фактори дорівнюють:

N=P; M_y=Pz_y; M_z=Py_p. (8.10)

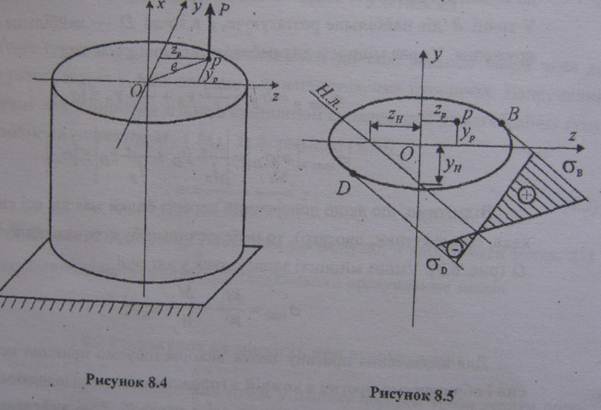
На основі принципу суперпозиції нормальне напруження а в довільній точці перерізу дорівнює сумі напружень від кожного силового фактору

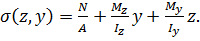(8.11)

Підставляючи (8.10) в (8.11), одержимо

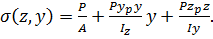(8.12)

Винесемо Р/А і врахуємо, що

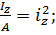
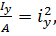
де і_z, i_y — головні радіуси інерції поперечногоперерізу стержня. Tоді

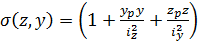. (8.13)

Формула (8.13) дає можливість знайти нормальні напруження в довільній точці поперечного перерізу стержня.

Тут z, у — координати довільної точки, а осі z, у вибирають так, щоб то­чка р лежала в 1-ій чверті.

Ми розглянули випадок, коли сила Р — розтягуюча. Якщо ж сила Р — стискаюча, то в формулі (8.13) перед Р треба записати знак мінус.

8.4 Розрахунок на міцність при позацентровому розтягу-стиску

Для визначення в даному перерізі небезпечних точок, треба знайти поло­ження нейтральної лінії. Для цього прирівняємо (8.13) до нуля і, скорочуючи на Р/ А, одержимо

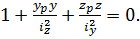(8.14)

Отже, нейтральна лінія є прямою, що не проходить через початок коорди­нат. Її положення доцільно визначати через відрізки, що відсікаються нею на координатних осях. Позначимо ці відрізки через z_н і у_н (рис. 8.5).

Підставляючи у формулу (8.14) по черзі у = 0 та z= 0, одержимо для них вирази

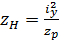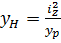; (8.15)

З співвідношення (8.15) видно, що нейтральна лінія перетинає координатні осі в точках, які належать квадранту, протилежному до того, в якому знаходи­ться точка р.

Якщо провести паралельно до нейтральної лінії дотичні до контуру перері­зу, то знайдемо найбільш небезпечні точки В і D (рис. 8.5), які найбільш віддалені від нейтральної лінії. Напруження в цих точках і умова міцності запишу­ться у вигляді

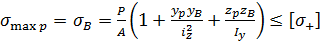
(8.16)

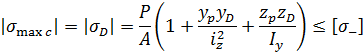
Де z_B, у _B і Z_D, y_D — координати точок В і D відповідно. Епюра напружень 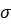показана на рис. 8.5.

Лекція 9

Дата добавления: 2014-01-04