Истоки заблуждений

Анализ истоков заблуждений начнем с фундамента так называемой Специальной теории относительности – преобразований Лоренца. Вот их классический вид [5], [6].

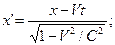(1)

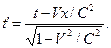(2)

Обратим внимание на то, что в формуле (1) присутствует координата 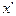, которая фиксируется в подвижной системе отсчета (рис. 1), а в формуле (2) - только время 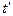, которое течет в этой же системе отсчета. Таким образом, в математических формулах (1) и (2) изменяющаяся величина пространственного интервала 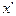в подвижной системе отсчета отделена, повторяю ещё раз отделена от времени 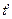, текущего в этой системе отсчета.

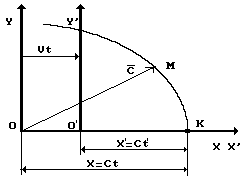
Рис. 1. Схема к анализу преобразований Лоренца

Теперь мы знаем, что в реальной действительности отделить пространство от времени невозможно, поэтому указанные уравнения нельзя анализировать отдельно друг от друга. Это - система уравнений и анализировать их необходимо вместе. Только такой анализ будет соответствовать Аксиоме Единства пространства - материи - времени, и результаты только такого анализа будут отражать реальность. Но это простое правило до сих пор игнорировалось Вами. Из уравнения (1) неявно следует, что при 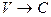величина пространственного интервала 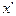уменьшается. Из этого физики ХХ века делали вывод, что с увеличением скорости 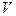движения подвижной системы отсчета величина пространственного интервала 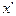сокращается. Далее, они брали для анализа одно уравнение (2)[1]. Из него также следует неявно, что при 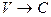величина 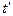уменьшается. Из этого они делали вывод о том, что с увеличением скорости движения подвижной системы отсчета темп течения времени 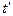в ней замедляется.

Исправим ошибочную интерпретацию. Поскольку в реальной действительности пространство от времени отделить невозможно, то проанализируем уравнения (1) и (2) совместно, для этого разделим первое на второе, в результате будем иметь

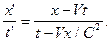(3)

Вот теперь математическая формула (3) отражает зависимость координаты 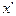от времени 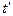. Из этого следует, что формула (3) работает в рамках Аксиомы Единства пространства - материи - времени, то есть в рамках реальной действительности. Обратим внимание на то, что материя в уравнении (3) присутствует косвенно. Её роль выполняют скорост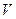и и 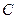. Обусловлено это тем, что скорость могут иметь только материальные объекты.

На рис. 1 видно, что 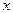- это координата положения светового сигнала в неподвижной системе отсчета. Она равна произведению скорости движения света 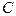на время 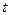. Если мы подставим 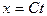в приведенную формулу (3), то получим координату 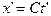, которая фиксирует положение светового сигнала в подвижной системе отсчета. Где же расположен этот сигнал? Поскольку мы изменяем координаты 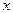и 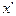, то в моменты времен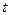и и 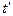он расположен на совпадающих осях 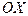и 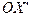, точнее - в точке 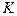- точке пересечения световой сферы с двумя осям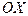и и 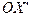(рис. 1).

Геометрический смысл преобразований Лоренца очень прост. В них зафиксированы координата 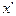точки 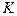в подвижной системе отсчета и её координата 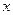в неподвижной системе отсчета (рис. 1). Это - точка пересечения световой сферы с осям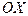и и 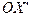. Вот и весь смысл преобразований Лоренца. Другой информации в этих преобразованиях нет и они не отражают никакие физические эффекты.

Важно и то, что приведённый анализ преобразований Лоренца придаёт всем математическим символам: , входящим в эти преобразования, четкий геометрический и физический смысл. Посмотрите внимательнее на рис. 1. При 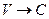величина 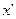действительно уменьшается. Вполне естественно, что уменьшается и время 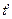, необходимое световому сигналу для того, чтобы пройти расстояние 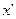. Вот Вам и причина парадокса близнецов. Приведите преобразования Лоренца к виду, соответствующему Аксиоме Единства пространства – материи – времени и все парадоксы исчезают.

А теперь представьте, сколько теорий и сколько математических моделей базируется на преобразованиях Лоренца, которые выполняют фактически роль теоретического вируса. Сколько ошибочных интерпретаций экспериментальных данных породили математические модели, зараженные этим вирусом!!!

Чтобы избавиться от этого вируса, обратим внимание на исключительно важный факт. Попытаемся разделить условно математические модели на математические и физико-математические. Назовем математические модели, содержащие только геометрические параметры, математическими, а те, в которых появляется время, - физико-математическими. Тогда уравнение сферы, содержащее только геометрические параметры

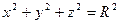(4)

назовем математическим.

Это же уравнение, но с переменным радиусом сферы 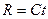автоматически становится физико-математическим.

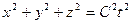. (5)

Мы ввели в математическую модель время. На примере анализа преобразований (1) и (2) Лоренца мы ясно увидели, что небрежное обращение с уравнениями, содержащими физический параметр время, очень дорого обходится человечеству. Поэтому проявим максимальную осторожность, анализируя следствия, вытекающие из математических моделей, содержащих время.

Не забывая изложенное, пойдем дальше. Конечно, нам желательно и даже обязательно знать истоки ошибочности преобразований Лоренца, а для этого надо проследить процесс их рождения, то есть вывода. Наиболее последовательно этот процесс описал Б. Робертсон в своей книге «Современная физика в прикладных науках» [6]. Он записал уравнение световой сферы в неподвижной системе отсчета в таком виде

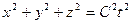. (6)

А уравнение этой же сферы в подвижной системе отсчета – в таком виде

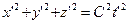. (7)

Далее, он записал

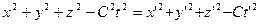(8)

и нашел, что это равенство выполняется при условии, если 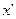определяется по формуле (1), 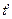- по формуле (2).

Грустно становится, когда читаешь это. Обращаем внимание на то, что это – физико-математическое равенство. Прежде чем получить его, необходимо уравнения (6) и (7) привести к такому виду:

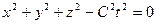; (9)

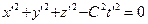(10)

и подумать какой результат мы получим при совместном решении этих двух уравнений, равных нулю? Что значит приравнять два нуля? Это значит - ничего не приравнять. Чтобы было что приравнивать, надо уравнения (7) и (8) записать так [2]:

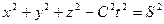; (11)

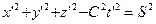. (12)

Вот теперь у нас появляются основания приравнять левые части уравнений (11) и (12). Но в таком виде они не принадлежат геометрии Евклида. Это - уравнения геометрии Минковского [7]. И мы обязаны проверить соответствие этой геометрии Аксиоме Единства. На рис. 2 показана схема для этой проверки.

Сравнивая уравнения (9) и (11), видим, что в геометрии Евклида 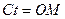- прямолинейная диагональ параллелепипеда (рис. 2), а в геометрии Минковского эта диагональ не может быть прямолинейной, так как это уравнение не соответствует теореме Пифагора. Присутствие в уравнении (11) величины 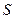делает диагональ параллелепипеда криволинейной ОЕМ (рис. 2). Фактически это означает, что параллельные прямые пересекаются. Вы видите, что началом этих идей является геометрия Лобачевского. Продолжим анализ.

Прямолинейность диагонали 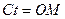в уравнении (9) соответствует свойству фотона двигаться в пространстве прямолинейно. Криволинейность же диагонали 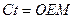в уравнении Минковского (11) противоречит этому свойству. Из этого следует, что мы не имеем права ставить скорость фотона в постулированное Минковским соотношение (11), которое является фундаментом его четырехмерной геометрии [7]. Проверим достоверность этого утверждения на простом примере. Для этого попытаемся определить координаты расположения светового сигнала в пространстве в момент времени в случае, когда . 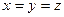Из уравнения (11) имеем

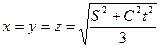. (13)

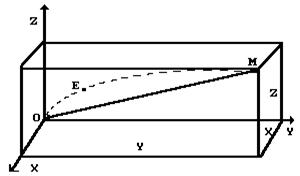
Рис. 2. Схема к анализу геометрии Минковского

Неизвестный пространственный интервал 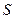исключает возможность определения координат 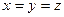. Уравнение (11) Минковского не позволяет определить положение фотона на траектории 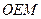в заданный момент времени 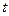, нарушая тем самым Единство пространства, материи и времени. Из этого следует неоспоримая ошибочность математической модели (11), которая является фундаментом четырехмерной геометрии Минковского.

Обратим внимание на то, что длина диагонали 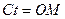измеряется с помощью фотона, движущегося прямолинейно со скоростью 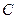[1], [2], поэтому, используя уравнение (9), мы можем определить положение фотона на диагонали 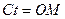в любой момент времени, что соответствует Аксиоме Единства пространства - материи - времени. В каждой точке диагонали 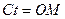фотон (материя), пространство и время находятся в неразрывном единстве. Например, для частного случая 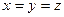уравнение (9) даёт такой результат

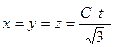. (14)

Для любого 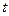мы можем найти координаты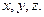

Теперь Вы видите, что истоком всех этих заблуждений является геометрия Лобачевского. Он придал статус аксиомы утверждению о том, что параллельные прямые пересекаются в бесконечности. Известно, что аксиома – это очевидное утверждение не имеющее исключений. Думаю, что среди Вас нет таких, кто согласится с тем, что утверждение о пересечении параллельных прямых в бесконечности является очевидным.

Обратим внимание ещё на один важный факт. В уравнении (9) используется символ 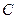- символ скорости фотона, который движется прямолинейно, что соответствует аксиомам Евклида, утверждающим, что между двумя точками можно провести только одну прямую линию и что параллельные прямые линии нигде не пересекаются. Этот факт согласуется с тем, что в уравнении (9) представлена теорема Пифагора, работающая в геометрии Евклида [8].

Введение пространственного интервала 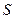в уравнении (11) автоматически превращает прямолинейную траекторию 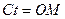в криволинейную 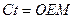, заставляя свет двигаться криволинейно. И сразу возникает вопрос: чему же равен радиус этой криволинейности? Ответа нет.

Трудно представить хаос, который бы существовал в мире, если бы свет двигался криволинейно. Ведь от далекой звезды до нашей матушки Земли можно провести лишь одну прямую и бесчисленное количество кривых и по какой из них движется свет, доходя до нас, остаётся тайной. Но физиков все это не смущало и они смело начали использовать преобразования Лоренца (1) и (2) для своих исследований. Причем они не утруждали себя анализом соответствия этих преобразований реальности. Они с небывалой лёгкостью использовали не только сами преобразования Лоренца, но и отдельные элементы этих преобразований. Часто можно встретить использование так называемого релятивистского корня 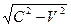. Не избежал этого искушения и Альберт Эйнштейн.

В основополагающей научной статье «К электродинамике движущихся тел» [9], на которую все релятивисты ссылаются, как на статью, положившую начало новой физике, он пишет: «Если принять во внимание, что свет вдоль оси 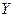при наблюдении из покоящейся системы всегда распространяется со скоростью 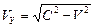, то….». Это утверждение может следовать из геометрии Минковского, но не из геометрии Евклида. Для проверки этого факта надо иметь схему, соответствующую, приведенной формуле, но в статье её нет. Восполним этот недостаток и нарисуем такую схему (рис. 3).

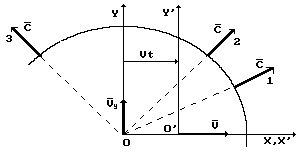
Рис. 3. Схема к анализу сути формулы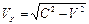

Вполне естественно, что формула

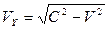(15)

следует из теоремы Пифагора, работающей в рамках аксиомы Единства пространства – материи – времени. Чтобы получить её из рис. 3, необходимо векторы скоростей 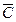фотонов 1 или 2 и скорость 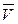подвижной системы отсчета (рис. 3) вернуть в точку О. Но у нас нет никакого права делать это.

Прежде всего, мы знаем, что можно переносить вдоль линии действия только векторы сил и то при условии, если все они действуют на одну изолированную систему [10]. В рассматриваемом случае векторы не сил, а скоростей. Они прикладываются непосредственно к тем точкам, скорость которых они описывают, и их нельзя переносить вдоль линии действия. Тем более, что в данном случае вектор 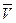приложен к началу О’ подвижной системы отсчета, которая автономна по отношению к фотонам, улетевшим из точки О в разных направлениях со скоростями света .

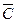Таким образом, мы не имеем ни математического, ни физического права возвращать векторы скоросте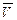й и 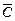в точку О, чтобы использовать теорему Пифагора для вывода формулы 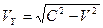. Отсутствие такого права подтверждает элементарная проверка. Полагая 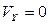, имеем абсурдный результат 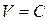. Если же мы возьмём скорость фотона 3 (рис. 3), улетевшего в левую часть световой сферы, то лишимся возможности получить и абсурдный результат.

Тем не менее, Нобелевский комитет выдаёт А. Эйнштейну Нобелевскую премию по физике со следующей формулировкой: «За важные физико-математические исследования, особенно за открытие закона фотоэлектрического эффекта» [11]. Дальше мы проанализируем и закон фотоэффекта и увидим правильность его математической модели, но ошибочность её интерпретации. Однако, ошибочность интерпретации мы должны признать естественной, так как в то время ещё не был открыт закон формирования спектров атомов и ионов, математическая модель которого полностью совпадает с математической моделью закона фотоэффекта [1], [2].

Теперь Вы представляете ущерб, нанесённый точным наукам учеными, согласившимися придать утверждению о пересечении параллельных прямых в бесконечности статус аксиомы без какой - либо экспериментальной проверки достоверности этого утверждения. К тому же это утверждение содержит явную логическую ошибку. Параллельные прямые пересекающиеся в бесконечности, автоматически перестают быть прямыми. Если в начале они были прямые и параллельные, то, пересекаясь в бесконечности, они перерождаются в криволинейные линии, что мы и наблюдаем в геометрии Минковского (11).

Хочу обратить Ваше внимание на то, что, критикуя сейчас А. Эйнштейна за его ошибочные теории относительности, Вы, как искатели научной истины, грешите. Его вина заключается лишь в том, что он с доверием отнесся к ошибочным результатам исследований своих предшественников и на этих ошибках создал свои, вполне естественно, ошибочные теории. Но начало ошибок положено не им, а Лобачевским, Риманом, Минковским, Лоренцем. Геометрию Римана мы не будем анализировать [12]. Это псевдоевклидова геометрия, поэтому она автоматически неприменима во всех исследованиях, где присутствует математический символ скорости света .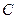

Думаю, что изложенного пока достаточно для того, чтобы осмыслить суть истоков фундаментальных научных заблуждений. Во второй лекции мы рассмотрим заблуждения Нильса Бора. Они скрыты очень глубоко и, тем не менее, мы найдем их.

ЛИТЕРАТУРА

1. Канарёв Ф.М. Начала физхимии микромира. Пятое издание. Краснодар 2004. 400 с.

2. Канарёв Ф.М. Начала физхимии микромира. Шестое издание. 500 с. Подготовлено к печати.

3. Ацюковский В.А. Общая эфиродинамика. М. «Энергоиздат». 1990. 278 с.

4. Канарёв Ф.М. Новый анализ фундаментальных проблем квантовой механики. Краснодар 1990, 174 с.

5. Бим Дж., Эрлих П. Глобальная Лоренцева геометрия. М. «Мир». 1985. 400с.

6. Робертсон Б. Современная физика в прикладных науках. М.: «Мир», 1985. 270с.

7. Сазанов А.А. Четырехмерный мир Минковского. М. «Наука» 1988. 220с.

8. Евклид. Начала Евклида. Книги I-VI. М-Л 1948г. 446с.

9. Эйнштейн А. К электродинамике движущихся тел. Сборник работ по специальной теории относительности. М.: «Атомиздат», 1973. с 97-116.

10. Канарёв Ф.М., Артёмов И.И., Зеленский С.А. Конспект лекций по теоретической механике. Краснодар, 2001. 265 с.

11. Храмов Ю.А. Физики. М. «Наука». 1983. 395с.

12. Рашевский П.К. Риманова геометрия и тензорный анализ. М. «Наука» 1967. 664 с.

Дата добавления: 2014-01-04