Текст лекции. Лекция 35. Решение задач на использование рекурсивных алгоритмов

Лекция 35. Решение задач на использование рекурсивных алгоритмов.

Краткая аннотация лекции.

В лекции рассматриваются опорные схемы решения задач рекурсивными способами, приводятся примеры разработки рекурсивных функций с помощью опорных схем.

Цель лекции: изучить рекурсивные алгоритмы и основные схемы решения задач рекурсивными способами, научиться применять рекурсивные алгоритмы при решении задач на языке C++.

В построении алгоритмов решения задачи важным является формирование общих подходов к выбору способа решения. Универсального метода, гарантирующего верный и оптимальный алгоритм решения для любой задачи, не существует. В частности, сведение решения к выбору итерационного или рекурсивного способа построения алгоритма зависит от результатов анализа постановки задачи. Поэтому необходимо иметь представление о возможных направлениях анализа решаемой задачи.

Разбиение задачи на подзадачи. Метод процедурной абстракции, положенный в основу процедурного программирования, предполагает выделение в задаче отдельных модулей, в дальнейшем реализуемых посредством функций. В процессе анализа задачи возможны случаи:

· разбиение условий задачи на части;

· разбиение требований задачи на части;

· разбиение области определения задачи на части.

Преобразования задачи. Последовательные преобразования решаемой задачи в цепочку эквивалентных задач сводятся к получению задачи, решение которой может быть получено более простым способом или уже известно. При этом эквивалентность задач понимается как совпадение их множеств решений, а преобразование должно не менять языка, ее записи. В противном случае это уже будет не преобразование, а моделирование.

Моделирование. В процессе работы над условием происходит замена исходной задачи ее моделью: текстовая задача переводится в уравнение, систему уравнений или неравенств. При этом проводится детальное исследование возможных ошибок или погрешностей метода, учет которых входит в алгоритмизацию задачи.

Введение вспомогательных элементов. В постановке задачи не всегда явно указывается набор данных, которые оказывают влияние на получение результата. Например, решение квадратного уравнения на множестве действительных чисел сводится к вычислению и анализу значения дискриминанта, о котором в постановке задачи ничего не сказано. Выделим следующие случаи:

· введение недостающих по смыслу задачи элементов между данными и искомыми элементами (дополнительное построение на чертеже, новые переменные для составления уравнений и т.п.);

· преднамеренное погружение задачи в большую размерность, то есть введение дополнительных параметров, не связанных с существом задачи.

С учетом вышеизложенного рассмотрим существующие подходы к выбору рекурсии как метода решения задач, то есть выделим основные опорные схемы рекурсивных вычислений:

· «Увидеть»;

· «Переформулировать»;

· «Обобщить»;

· «Использовать характеристическое свойство»;

· «Перенести часть условий в проверку»;

· «Обратить функцию»;

· «Найти родственника».

Опорные схемы по своей сути не являются реальной классификацией методов решения задач с использованием рекурсии. Одна и та же задача, исследуемая с опорой на разные схемы, может приводить к одному и тому же рекурсивному алгоритму. Более того, иногда достаточно трудно однозначно утверждать, что при решении задачи применялась именно конкретная схема. Однако опорные схемы определяют подходы к анализу условия задачи, опираясь на которые можно выработать метод ее решения.

Опорная схема «Увидеть»

Данная опорная схема является наиболее естественной, так как содержится в постановке задачи. Для разработки триады достаточно использовать параметры, тривиальный случай и соотношения, непосредственно вытекающие из условия.

Опорная схема «Переформулировать»

Часто в условии задачи не только не обозначена рекурсия, но и сама задача не является алгоритмически сформулированной. Иногда ее простая перефразировка, а чаще построение математической модели позволяют обнаружить первоначально скрытую рекурсию.

Рассмотрим задачу о динамике вклада. Большой выбор простых содержательных задач, допускающих рекурсивное решение, можно встретить в сфере банковской деятельности. Рассмотрим несколько различных рекурсивных вариантов решения задачи о динамике вклада.

Вкладчик положил в банк сумму в sum денежных единиц под p процентов за один период времени. Составим функцию, возвращающую величину вклада по истечении n периодов времени.

Вычисление значения величины вклада можно проводить по известной формуле сложных процентов: 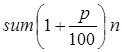. Но рассмотрим рекурсивный вариант алгоритма решения задачи.

Параметризация: выбор параметров следует непосредственно из условия задачи, то есть sum – первоначальный размер положенной суммы, p – процент вклада, n – количество периодов хранения вклада.

База рекурсии: для 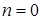размер суммы не изменится, то есть останется sum.

Декомпозиция: если 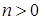, то размер вклада вычисляется как сумма за 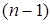периодов, увеличенная на процент p.

float Deposit(float sum, float p, int n){

if(n==0) return sum; //база рекурсии

return Deposit(sum,p,n-1)*(1+p/100); //декомпозиция

}

Общее количество рекурсивных вызовов при вычислении Deposit(sum, p, n) равно n. Можно уменьшить это значение до величины порядка 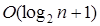исходя из следующих двух декомпозиционных посылок, описывающих случаи четного и нечетного n.

float DepositNew(float sum, float p, int n){

if (n==0) return sum;// база рекурсии

if (n%2==0) //декомпозиция для четного n

return sum*pow(DepositNew(1.0,p,n/2),2);

//декомпозиция для нечетного n

return sum*(1+p/100)*DepositNew(1.0,p,n-1);

}

Опорная схема «Обобщить»

Если из постановки задачи рекурсию извлечь не удается, то за счет перехода к ее некоторому обобщению иногда это сделать возможно. Как правило, это обобщение протекает за счет введения дополнительных параметров, то есть намеренного погружения исходной задачи в пространство большей размерности, чем это обусловлено ее основными параметрами. Поэтому данную опорную схему иногда называют «Погрузить» или «Вложить». Использование рассматриваемой схемы предполагает, что из решения обобщенной задачи может быть получено решение исходной задачи. В некоторых случаях данная схема может быть использована для улучшения быстродействия алгоритма или для перехода от одного типа рекурсии к другому. При этом «Обобщение» является наиболее общей и часто используемой схемой при решении многих задач рекурсивными алгоритмами.

Стоит отметить еще одно обстоятельство, связанное с данной схемой. Имея свободу выбора обобщения исходной задачи, мы, тем не менее, ограничены жесткими рамками, регламентирующими этот выбор: решение (доказательство) обобщения должно быть по возможности простым и из него должно легко выделяться решение исходной задачи.

Рассмотрим задачу под названием «Абракадабра». Последовательность из латинских букв строится следующим образом. На нулевом шаге она пуста. На каждом последующем шаге последовательность удваивается, то есть приписывается сама к себе, и к ней слева добавляется очередная буква алфавита (a, b, c, …). По заданному числу n определить символ, который стоит на n -м месте последовательности, получившейся после шага 26.

Приведем первые шаги формирования последовательности: 0 - пустая последовательность, 1 - «a», 2 - «baa», 3 - «cbaabaa», 4 - «dcbaabaacbaabaa» и так далее по закономерности. Данный процесс носит рекурсивный характер.

Параметризация. Построим более общую функцию, чем это требуется по условиям задачи. Пусть значение функции Abra(k,n) - n -я буква в последовательности, полученной на шаге k (k = 1, …, 26). Будем возвращать значение функции в виде целочисленного кода, соответствующего требуемому символу.

База рекурсии. Значение Abra(k,1) равно k -й букве латинского алфавита. Этот факт можно взять в качестве базы рекурсии.

Декомпозицию удобно организовать по k, проводя «раскрутку» последовательности по шагам в обратном направлении. Это приводит к следующей зависимости:

· если 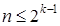, то искомый символ находится на 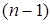месте в латинском алфавите;

· если 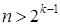, то искомый символ находится на 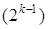месте в латинском алфавите.

int Abra(int k, int n){

if (n > pow(2, k-1)-1 || k > 26) return 0;

//корректность входных данных

if (n == 1) return k+96; //база рекурсии

return Abra(k-1, n-(n <= pow(2, k-1)? 1: pow(2, k-1)));

//декомпозиция

}

Опорная схема «Характеристические свойства»

Совокупность всех или части условий любой задачи, оформленная в виде некоторого предиката над наборами входных данных и возможных результатов, назовем характеристическим свойством задачи. Если в предикате задействованы все условия задачи, то характеристическое свойство и соответствующий предикат назовем полным, если нет, - частичным. Формальная запись полного или частичного предиката, с одной стороны, позволяет проводить независимую проверку правильности работы ранее разработанных алгоритмов решения данной задачи, а с другой стороны, может оказать существенную помощь для отыскания новых рекурсивных алгоритмов ее решения. Остановимся на примерах, иллюстрирующих второй вариант использования характеристических свойств задачи.

Рассмотрим задачу о «Допустимых последовательностях». Последовательность длины N, составленная из символов 0 и 1, называется допустимой, если в ней нет двух подряд идущих символов 1. В противном случае называется недопустимой. Определим 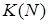- общее количество допустимых последовательностей для натурального значения N.

Методом полного перебора эту задачу можно решить лишь при небольших значениях N, так как количество всевозможных последовательностей равно .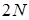

Пусть набор представлен в виде вектора v с компонентами 0 и 1 (с нумерацией их от 0 до 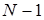). Определим предикат 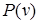, истинный только на допустимых наборах v. Формализованная запись этого предиката выглядит следующим образом:

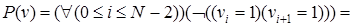
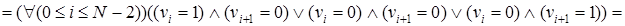
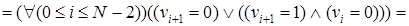
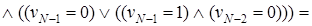
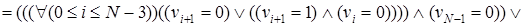
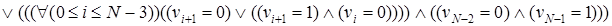
Фактически формальными преобразованиями предиката мы получили его декомпозицию, то есть множество 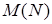допустимых векторов длины N (N ³ 3) можно представить в виде объединения двух непересекающихся подмножеств:

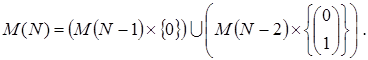
Здесь под декартовыми произведениям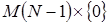и и понимаются множества векторов длины N. В первом случае последняя компонента векторов равна 0, а первые 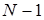компонентов составляют допустимые векторы длиной 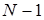. Во втором случае последние две компоненты равны соответственно 0 и 1, а первые 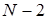компоненты составляют допустимые векторы длины 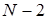. Кроме того: 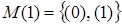; 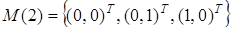. Отсюда вытекает справедливость следующего рекуррентного соотношения:

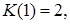
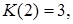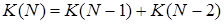, (N ³ 3).

Таким образом, 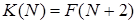, то есть искомая последовательность 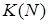есть сдвиг последовательности Фибоначчи 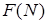на два элемента влево. Для вычисления 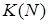можно написать рекурсивную функцию, аналогичную функции вычисления членов последовательности Фибоначчи.

Опорная схема «Перенести часть условий в проверку»

Во многих задачах, сводящихся к рекурсивным алгоритмам, рекурсия в явном виде сразу не обнаруживается или достаточно сложна для алгоритмической реализации. Однако удаление части условий из задачи приводит к новой вспомогательной задаче, рекурсивный алгоритм решения которой строится достаточно несложно. В этом случае чтобы узнать, является ли полученный для новой задачи ответ (ответы) решением исходной задачи, необходимо проверить, выполняются ли для него ранее удаленные условия или нет.

Если решение задачи сводится к вычислению значения истинности некоторого предиката, непосредственно построенного из конъюнкции условий задачи на наборах входных данных, то описанная схема допускает возможность проверки выполнимости удаляемых условий как до использования рекурсивного алгоритма решения вспомогательной задачи, так и после этого. При этом рассматриваемая опорная схема может использоваться как конкретная разновидность схемы «Обобщить». Перенося одно или несколько условий исходной задачи в проверку, то есть, фактически временно отбрасывая их, мы получаем новую задачу, являющуюся естественных обобщением решаемой задачи. Иногда бывает удобно или более естественно схему «Перенести часть условий в проверку» интерпретировать как разновидность схемы «Переформулировать».

Опорная схема «Обратить функцию»

Задачи на обращение функций являются достаточно распространенными. Иногда возникает вопрос об обращении функций, заданных посредством алгоритмов. Пусть, например, относительно параметра 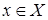решается уравнение вида 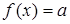при некотором известном рекурсивном алгоритме f и заданной величине , где X и Y - множества. Тогда знание обратной для f рекурсивной функции 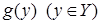сразу же позволило бы решить исходное уравнение: , , .

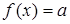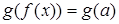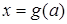Поэтому умение «обратить» алгоритм является хотя и непростым, но достаточно полезным и эффективным подспорьем в решении задач рекурсивными методами. Реальное использование данной опорной схемы проводится так. Алгоритм решения исходной задачи нам неизвестен. Возможно, он не подходит по причине сложности или плохой эффективности. Однако для какой-либо из обратных для решаемой задачи удается построить алгоритм решения. В некоторых случаях простые рассуждения, приводящие к незначительным изменениям обратной задачи, позволяют получить конкретный искомый алгоритм.

Для рассуждений и изменений сложно дать какие-либо общие рекомендации, так как они жестко связаны с содержанием рассматриваемой задачи, выбором для нее обратной задачи и алгоритма решения. Многое здесь зависит от того, какую из обратных задач мы выбрали.

Опорная схема «Найти родственника»

Иногда исходная задача естественным образом распадается на две или более вспомогательные родственные задачи так, что в совокупности, взаимно дополняя друг друга, они уже будут определять вполне просматриваемую косвенную рекурсию.

Рассмотрим пример, связанный с экзотическими средними. Пусть и 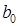- два положительных числа (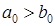). Составим их среднее арифметическое и среднее геометрическое. Продолжим этот процесс рекурсивно. Если числа 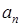и 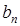уже построены, то определим и 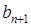следующим образом:

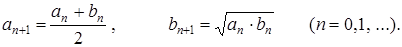
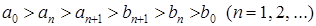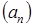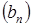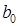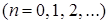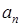Можно показать, что . Откуда вытекает, что обе последовательности и с двух разных сторон монотонно стремятся к общему пределу, который называют средним арифметико-геометрическим или экзотическим средним исходных чисел и . Таким образом, при любом заданном n числа и 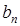служат приближениями сверху и снизу для среднего арифметико-геометрического и 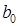. Для поиска экзотического среднего можно составить функцию, реализующую косвенную рекурсию. При этом параметризация, база и декомпозиция в явном виде приведены в задаче.

#include "stdafx.h"

#include <iostream>

using namespace std;

float Arifm(int n, float a, float b);

float Geom(int n, float a, float b);

int _tmain(int argc, _TCHAR* argv[]){

int n;

float a,b;

do {

printf ("a>0, a=");

scanf("%f",&a);

printf ("b>0, b=");

scanf("%f",&b);

printf ("n>0, n=");

scanf("%d",&n); }

while (a<=0 || b<=0 || n<=0);

printf("Exotic: between %f and %f",

Arifm(n,a,b),Geom(n,a,b));

system("pause");

return 0;

}

float Arifm(int n, float a, float b){

if (n==0) return a;

return (Arifm (n-1,a,b)+Geom(n-1,a,b))/2;

}

float Geom(int n, float a, float b){

if (n==0) return b;

return pow(double(Arifm (n-1,a,b)*Geom(n-1,a,b)),0.5);

}

Дата добавления: 2014-01-04