Завдання

1. Визначте, які з наведених тверджень справедливі:

а) |{Æ}| = 1;

б) {{Æ}} Î {{{Æ}}};

в) |{{Æ}}| = 2;

г) x Î { x };

д) { x } Í { x };

е) { x } Î { x };

ж) { x } Î {{ x }}.

2. Скільки елементів містять такі множини:

а) { x };

б) {{ x }};

в) { x, { x }};

г) {{ x }, x, {{x, {x}}}}.

3. Які з наведених тверджень правильні? Доведіть

а) якщо А Ì В і В Ì С, то А Ì С;

б) якщо А Í В і В Í А, то А = В;

в) якщо А Í В і В Í С, то А Í С.

4. Дана множина D = {7, 13, 25, 34, 101, 112}. Які з наведених множин є підмножинами множини D?

а) {1, 7, 13};

б) {0, 1, 12};

в) {25, 112, 34};

г) { а, b, с, n };

д) {7, 13, 25, 34, 101, 112}.

e) Æ.

5. Визначте, які з наведених множин дорівнюють одна одній:

а) А = { х | існує у такий, що х = 2 y, у Î N };

б) С = {1, 2, 3};

в) D = {0, 2, -2, 3, -3, 4, -4,...};

г) E = { 2х | х Î Z}.

6. Побудуйте 2^а для множини А, якщо:

а) А = {{Æ}};

б) А = {1, 2, 3, 4};

в) А = {«день», «ніч»};

г) А = {1, {2, 3}, 4}.

7. Скільки підмножин містить:

а) множина днів тижня;

б) множина місяців року.

8. Нехай задані множини S_{n -1} і S _n, такі, що S _{n -1} = { а ₀, а ₁..., а_{n -1}}, S _n = { а ₀, а ₁..., а_n }. Поясніть, як одержати з множини 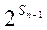множину .

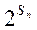9. Складіть алгоритм, який як вхідні дані одержує дві множини і визначає, чи рівні ці множини, чи є одна з них підмножиною другої.

10. Складіть алгоритм, який як вхідні дані одержує множину і конструює список всіх можливих підмножин даної множини.

1.3. Геометрична інтерпретація множин

Діаграми Венна, круги Ейлера

Для наглядного зображення співвідношень між підмножинами універсальної множини використовуються діаграми Венна і круги Ейлера.

Побудова діаграми Венна полягає в розбитті площини на 2 ⁿ областей за допомогою п фігур. Кожна фігура на діаграмі зображує окрему множину, п — число зображуваних множин. При цьому кожна наступна фігура повинна мати одну і тільки одну загальну область-перетин з кожною з раніше побудованих фігур. Площина, на якій зображуються фігури, становить універсальну множину U. Таким чином, точки, що не належать жодній з фігур, належать тільки U. Діаграма Венна для двох множин А і В зображена на рис. 1.1.

За допомогою діаграм Венна можна графічно показати, чи належить деякий елемент х Î U розглянутим множинам, чи ні. Наприклад, на рис. 1.1 елемент x ₁ належить А і не належить В, х ₂ належить А і В, х ₃ належить В і не належить А, х ₄ не належить ні А, ні В. Будь-який елемент належить універсальній множині U.

Діаграму Венна для трьох множин А, В і С зображено на рис. 1.2, де елемент х ₁ належить множинам А, В і С, х ₂ належить В і С і не належить А.

Діаграму Венна для чотирьох множин А, В, С і D зображено на рис. 1.3, на якому як приклад зображено елемент x ₁, що належить всім чотирьом множинам: А, В, С і D. Для ясного уявлення заштрихуємо кожну область цієї діаграми, використовуючи більш густе штрихування там, де точки належать більшому числу множин:

§ належить тільки одній з множин;

§ належить тільки двом з множин;

§ належить тільки трьом з множин;

§ належить всім чотирьом множинам.

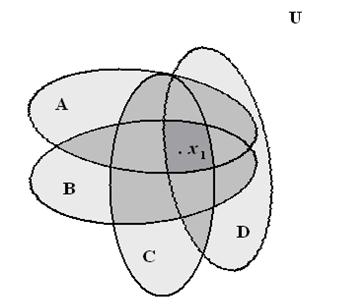
Рис. 1.3. Діаграма Венна для чотирьох множин А, В, С і D

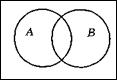
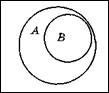
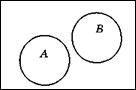
Діаграми Венна не відображають реальні відношення включення, що встановлені між множинами, а розглядають їх у загальному випадку. Індивідуальні відношення між заданими множинами зображують за допомогою кругів Ейлера. В цьому випадку множини, що не мають загальних елементів, зображують не перетинними фігурами. Відношення включення на множинах зображують, розташовуючи одну фігуру вкладеною в іншу. Розглянемо побудову кругів Ейлера на прикладі рис 1.4.

А = {1, 4, 6}; В = {1, 5, 8}; Загальний елемент — 1	А = {1, 4, 6}; В = {1, 6}; В Í А	А = {1, 4, 6}; В = {3, 5, 8}; Немає загальних елементів А і В

Рис. 1.4. Зображення множин за допомогою кругів Ейлера

Дата добавления: 2014-01-04