Основные законы распределения наработки до отказа

Экспоненциальное распределение. Непрерывная случайная величина — наработка системы до отказа может описываться различными законами распределения взависимости от свойств системы и ее элементов, условий работы, характера отказов и др. Наибольшее распространение получило экспоненциальное (показательное) распределение, при котором функция распределения наработки до отказа

F (t) = l – е, (1. 21)

где — параметр этого распределения.

Согласно (1.5) соответствующая плотность распределения

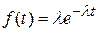, (1. 22)

Согласно (1.3) функция надежности

P(t)= е. (1.23)

Согласно (1.7) и (1.9) вероятность отказа системы до момента t 1 и вероятность безотказной работы до момента t\ соответственно будут

; ;

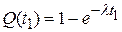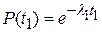Согласно (1.17} средняя наработка до отказа

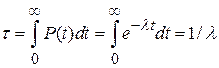, (1.24)

т. е. равна величине, обратной параметру экспоненциального распределения.

Подставив в (1.19) плотность распределения (1.22), после двукратного интегрирования по частям найдем дисперсию наработки до отказа

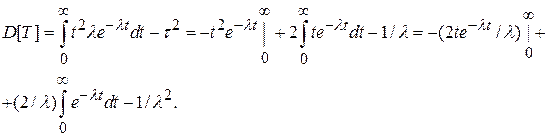
Из (1.13) следует, что интенсивность отказов

является постоянной величиной, не зависящей от времени и численно равной параметру распределения и, как видно из (1.24), обратной средней наработке до отказа.

Отметим одно характерное свойство, присущее только экспоненциальному распределению: вероятность Р (t 1, t 2) безотказной работы системы на интервале (t 1, t 2) (при условии, что в момент t 1 система работоспособна) зависит только от длины интервала t 2 – t 1 и не зависит от времени t 1 предшествующей работы системы, т. е. от ее “возраста”. Чтобы это доказать, достаточно в (1.11) подставить значение (1.23):

. (1.25)

Так как для экспоненциального закона характерно постоянство интенсивности отказов = const, то область применения этого закона – системы и элементы, где можно не учитывать ни период приработки, ни участок старения и износа (например, многие средства вычислительной техники и регулирования). Можно показать, что экспоненциальное распределение хорошо описывает время безотказной работы сложных систем, состоящих из большого числа разнородных компонентов. Наконец, одна из основных причин широкого использования экспоненциального закона заключается в том, что вследствие неизменности величины расчеты надежности при применении этого распределения наиболее просты.

Нормальное распределение. В отличие от экспоненциального нормальное распределение используют для описания таких систем и особенно их элементов, которые подвержены действию износа. Функция и плотность распределения наработки до отказа Т при этом соответственно будут

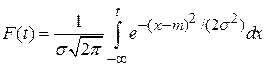; (1. 26)

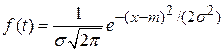, (1.27)

где 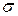и т – параметры нормального распределения.

Пользуясь соотношениями (1.16) и(1.19), можно показать, что при нормальном распределении средняя наработка до отказа и дисперсия наработки до отказа будут

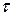= m; D [ T ] =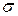². (1. 28)

Для практического использования соотношений (1.26) и (1.27) перейдем от случайной величины Т к иной случайной величине

Z= (T–m) /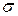, (1. 29)

имеющей математическое ожидание M [ Z ] = 0 и дисперсию D [ Z ] = 1.

Согласно правилам определения закона распределения функции случайного аргумента (см. [16]) плотность распределения величины Z следует из (1.27) и (1.29):

.

Соответственно функция распределения величины Z

.

Очевидно, что функция 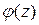является симметричной, т. е. 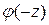=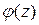, а следовательно,

В таблицах часто приводят значения не функции Ф (z), а несколько иной функции

. (1.30)

Функции Ф (z) и Ф ₀ связаны между собой соотношением

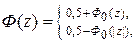
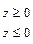(1.31)

Приведем значения функции (1.30) для нескольких положительных z:

Ф ₀(0,5) = 0,191; Ф ₀(1) = 0,343; Ф ₀(2) = 0,477.

Нормальное распределение, как это видно из соотношения (1.26), описывает поведение случайных величин в диапазоне (-,). Однако наработка до отказа является неотрицательной величиной, чтобы это учесть, вместо нормального в принципе должно использоваться усеченное нормальное распределение. Область возможных значений случайной величины Т может быть различной; ниже примем, что эта область (0, ), и проведем усечение распределения в точке t = 0. Тогда функция распределении случайной величины Т имеет вид

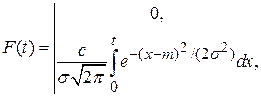
где с — нормирующий множитель; 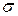, т — параметры распределения.

При этом плотность распределения

.

Значение с выбирают из условия, что площадь под кривой плотности распределения равна единице. Использовав подстановку (1.29), можно показать, что

.

В усеченном нормальном распределении средняя наработка до отказа и дисперсия наработки до отказа

; ,

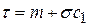где .

Усеченное нормальное распределение обычно применяют, если m <3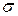. В противоположном случае использование более простого нормального (неусеченного) распределения дает достаточную точность.

Распределение Вейбулла–Гнеденко. Втеории надежности получило применение распределение Вейбулла–Гнеденко, описываемое функцией и плотностью распределения соответственно

; .

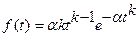Это двухпараметрическое распределение, где параметр k определяет вид плотности распределения, параметр – его масштаб. Так, при k= 1распределение Вейбулла–Гнеденко совпадает с экспоненциальным когда интенсивность отказов постоянна; при k > 1интенсивность отказов монотонно возрастает, при k < 1монотонно убывает. Распределение Вейбулла–Гнеденко может быть применено для описания наработки до отказа ряда электронных и механических технических средств, включая период приработки.

Соотношения для определения показателей надежности для трех рассмотренных выше распределений даны в табл. 1.2.

Таблица 1.2

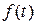
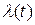
Распре-деление	Функция надёжности P (t)	Плотность распределения	Интенсивность отказов	Средняя наработка до отказа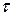
Экспонен-циальное
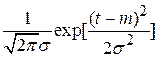
Нормаль- ное			см. прим.
Вейбулла-Гнеденко

Примечание: ,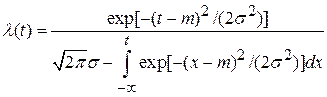

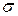, , , , – параметры соответствующих распределений; Г-гамма функция

Дата добавления: 2014-01-04