Тема 1.4. Показатели надежности ремонтируемых объектов

ЛЕКЦИЯ 3

Восстанавливаемую систему целесообразно рассматривать как систему массового обслуживания, в которой поток заявок на обслуживание представляет собой поток отказов аппаратуры. Каналами обслуживания являются ремонтные бригады, восстанавливающие работоспособность аппаратуры.

Будем считать, что поток заявок на обслуживание - пуассоновский.

Поток восстановлений - также пуассоновский.

В этом случае для анализа надёжности восстанавливаемой системы можно использовать теорию марковских случайных процессов.

Имеем нерезервированную восстанавливаемую систему, состоящую из одного элемента. Система находится под действием пуассоновского потока отказов с интенсивностью l. После отказа система начинает немедленно восстанавливаться (ремонтироваться). Поток восстановлений - пуассоновский с интенсивностью m.

В любой момент времени система может находиться в одном из двух состояний:

- состояние работоспособности,

- состояние отказа (ремонта),

- вероятность нахождения системы в состоянии ,

- вероятность нахождения системы в состоянии .

Требуется определить функцию готовности 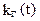и функцию простоя нерезервированной восстанавливаемой системы.

Функция готовности совпадает с вероятностью работоспособного состояния, т.е.

=.

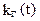Функция простоя совпадает с вероятностью отказа, т.е.

= .

Составим систему дифференциальных уравнений Колмогорова. Имеем

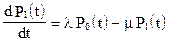(2.1)

Предположим, что при t = 0 система находилась в работоспособном состоянии, т.е.

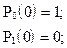
Для любого момента времени t имеем

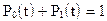(2.2)

Из двух уравнений (2.1) одно является лишним, т.к. 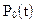и 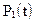связаны соотношением (2.2). Учитывая это, отбросим второе уравнение, а в первое уравнение вместо 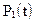подставим 1 - 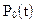. Имеем:

или (2.3)

Будем искать решение уравнения при ненулевых начальных условиях.

Запишем решение уравнения (2.3). Имеем:

или

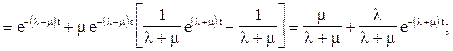
Таким образом

Определим 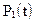. Имеем: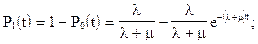

Таким образом:

При длительной эксплуатации, т.е. при t ® ¥ имеем:

где - коэфициент готовности системы, 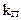- коэфициент простоя системы.

Учитывая, что

, .

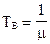где 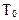- среднее время безотказной работы системы;

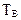- среднее время восстановления (ремонта) системы,

имеем

; ;

, ;

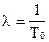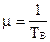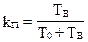Таким образом, коэффициент готовности характеризует долю времени, в течении которого система работоспособна. Коэффициент простоя характеризует долю времени, в течении которого система ремонтируется.

Определим коэффициент готовности и коэффициент простоя системы, содержащей основной и n - 1 резервных элементов, находящихся в нагруженном режиме. Отказавшие элементы образуют очередь на ремонт, который осуществляется одной бригадой с интенсивностью m. Интенсивность отказа любого элемента равна l.

Введём в рассмотрение состояния , , ………., :

- работоспособны все n элементов

- отказал один элемент, остальные работоспособны

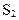- отказали два элемента, остальные исправны

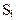- отказали i элементов, остальные исправны

…………………………………………………….

- отказала вся система, т.е. отказали все n элементов.

Построим граф состояния системы.

Составим систему дифференциальных уравнений Колмогорова. Имеем:

……………………………………….

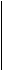
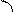
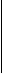
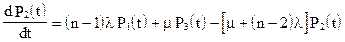
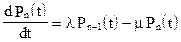
где 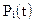- вероятность нахождения системы в момент времени t в состоянии 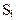, i = 0,1…, n

В установившемся режиме имеем:

;

;

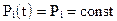В результате получим систему алгебраических уравнений вида:

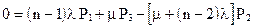
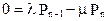
Из системы алгебраических уравнений имеем:

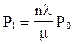
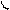
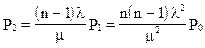
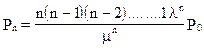
Для вероятностей состояний справедливо следующее соотношение

;

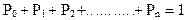Определим 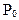. Имеем:

.

;

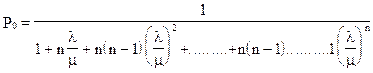или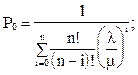

Отсюда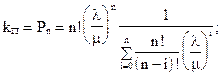

Коэффициент готовности:

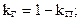
Дата добавления: 2014-01-04