Властивості ланцюгів Маркова

Відзначимо тепер деякі властивості марковських ланцюгів, які стосуватимуться лише ергодичних та поглинаючих скінченних ланцюгів Маркова. Доведення сформульованих нижче тверджень опускаємо (їх можна знайти, наприклад, в [4], а також в додатковій літературі, яка наведена в кінці даного розділу).

Ергодична властивість. За деяких умов у ланцюгу Маркова із зростанням (номера кроку) встановлюється стаціонарний режим, в якому система продовжує блукати по станах, проте ймовірності цих станів вже не залежать ні від номера кроку, ні від початкового розподілу ймовірностей. Такі ймовірності називаються граничними (або фінальними) ланцюга Маркова. Надалі фінальні ймовірності позначатимемо через 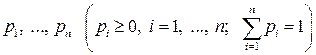, а вектор 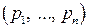, координатами яких є граничні ймовірності 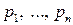будемо називати граничним (або фінальним) вектором.

Наступна теорема описує широкий клас марковських ланцюгів, які володіють наступною властивістю: граничні ймовірності 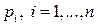, не тільки існують, утворюють розподіл ймовірностей 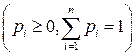, але і такі, що для всіх 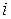(такі розподіли називаються ергодичними).

Теорема (ергодична теорема). Нехай – матриця перехідних ймовірностей ланцюга Маркова зі скінченною множиною станів . Тоді, якщо ланцюг Маркова ергодичний, то існують числа 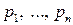, такі, що

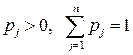(23)

і для будь-якого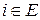

. (24)

Навпаки, якщо існують числа 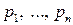, що задовольняють умови (23), (24), то ланцюг Маркова ергодичний.

Числа 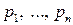є єдиним розв’язком системи рівнянь

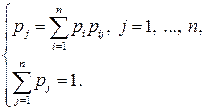(25)

Система рівнянь (25) відіграє важливу роль в теорії ланцюгів Маркова. Кожний її невід’ємний розв’язок 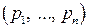прийнято називати стаціонарним або інваріантним розподілом ймовірностей для марковського ланцюга з матрицею перехідних ймовірностей 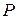. Пояснення цієї назви полягає в наступному.

Візьмемо розподіл 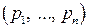в якості початкового, . Тоді

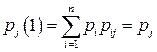
і взагалі . Іншими словами, якщо в якості початкового розподілу взяти 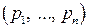, то цей розподіл не буде змінюватися зі зміною числа кроків (з часом), тобто для будь-якого

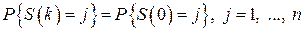
Відзначимо, що стаціонарний розподіл ймовірностей (і до того ж єдиний) може існувати і для неергодичних ланцюгів. Справді (див. приклад 10), якщо

,

то

,

і, отже, границі 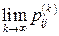не існують. У той же час система рівнянь (25) перетворюється в систему

єдиним розв’язком якої є .

Властивості поглинаючих ланцюгів Маркова. Такого типу ланцюги були визначені в п. 2.3 як такі, що складаються лише з незворотних та поглинаючих станів. Система, що описується подібним ланцюгом Маркова, поступово переходить з незворотних станів у поглинаючі, знаходячись у незворотних станах деякий випадковий час. Очевидно, що коли такий ланцюг містить всього станів, з яких – поглинаючих, то при відповідній нумерації станів його матриця перехідних ймовірностей 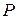може бути зображена у вигляді

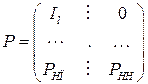, (27)

де ; – одинична матриця з порядком 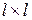; 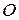– матриця з порядком 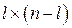, що складається з нулів; 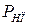– матриця з порядком 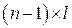, яка задає ймовірності переходу з незворотних станів у поглинаючі; 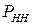– матриця з порядком 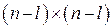, що складається з ймовірностей переходу між незворотними станами. Припустимо, що нас цікавлять характеристики:

• – середнє значення числа кроків , протягом яких система, яка вийшла з незворотного стану 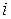, перебуває в незворотному стані ;

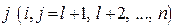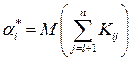• – середнє число кроків, протягом яких ланцюг Маркова перебуває в незворотних станах, якщо вихідним є незворотний стан ;

• – ймовірність того, що система, яка вийшла з незворотного стану 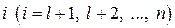, попаде в поглинаючий стан .

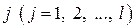Для поглинаючих ланцюгів Маркова, що задаються матрицями перехідних ймовірностей вигляду (27), справедливі наступні властивості:

1) значення визначаються як відповідні елементи матриці

, (28)

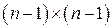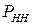де – одинична матриця з порядком ; а – матриця ймовірностей переходу між незворотними станами з (27);

2) значення визначаються як відповідні компоненти вектора-стовпця

, (29)

де 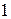– вектор-стовпчик з порядком , компоненти якого дорівнюють одиниці, а – матриця, визначена співвідношенням (28):

Наслідок. Якщо початково ланцюг Маркова знаходиться в незворотному стані 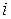з ймовірністю 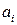, так що початковий розподіл ймовірностей незворотних станів ланцюга Маркова задається вектором , то середнє число кроків до поглинання 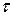визначається за формулою

; (30)

3) значення ймовірностей визначаються як відповідні елементи матриці:

, (31)

де – матриця, визначена співвідношенням (28), а 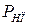– матриця з (27), яка задає ймовірності переходу з незворотних станів у поглинаючі.

Властивості ланцюга Маркова, який містить множину незворотних станів 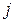і замкнену (поглинаючу) множину зворотних станів .

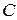При аналізі такого типу ланцюгів нас можуть цікавити наступні питання:

• яка ймовірність того, що система, розпочинаючи блукання з незворотного стану, весь час буде знаходитися в множині незворотних станів?

• як обчислити ймовірність того, що система, яка виходить з незворотного стану 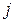, коли-небудь досягне поглинаючу множину зворотних станів ?

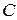Відповіді на ці питання містяться в наступних твердженнях:

Твердження 1. У скінченому ланцюгу Маркова ймовірність того, що система весь час буде знаходитися в множині незворотних станів дорівнює нулю.

Твердження 2. Ймовірність визначається як єдиний розв’язок системи лінійних рівнянь:

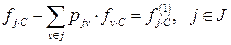. (32)

У цій системі сумування відбувається по всіх незворотних станах ланцюга, а – це ймовірність перейти з 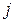у будь-який зі станів множини 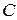за один крок.

Зауваження. У п. 2. поза нашою увагою залишилися такі важливі розділи теорії марковських процесів як процеси з дискретними станами та неперервним часом і процеси з неперервними станами та неперервним часом. Такі процеси також знаходять широке застосування в економічній практиці. Зокрема, марковські процеси з дискретними станами та неперервним часом використовуються при моделюванні систем масового обслуговування. Далі, важливий клас марковських процесів з неперервними станами та неперервним часом становлять дифузійні процеси, які використовуються при побудові економіко-математичних моделей для задач, що зустрічаються у фінансовій та страховій математиці.

Дата добавления: 2014-01-04