Лекція №11

Тема: "Метод фазової площини"

Метод полягає в дослідженні руху зображеної точки на фазовій площині. В якості змінних, відкладених по осях абсцис і ординат площини використовують керовану величину 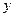і швидкість її зміни 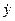або похибку системи 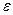і швидкість її зміни 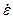або інші.

Фазовою площиною називається площина, на якій по двох осях відкладені дві змінні, що характеризують поведінку автоматичної системи (лінійної або нелінійної) в динаміці (у перехідному процесі).

За дві такі змінні найчастіше розглядають відхилення (похибку) регульованої вихідної величини х і швидкості зміни цього відхилення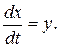

У більш загальному випадку стан автоматичної системи описується точкою в n–мірному просторі, де n – порядок характеристичного рівняння, що описує лінійну частину системи. Точка в такому просторі з n координатами називається зображуючою точкою. А простір називається простором станів або фазовим простором. Осями простору є х та її похідні:

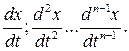
У врівноваженому стані зображуюча точка знаходиться у спокої. Під час перехідного процесу (ПП) змінна х і її похідні змінюються, та зображення точки рухається. Кожному ПП відповідає певна траєкторія, яка називається фазовою. Позиція, з якої починається рух точки, визначається початковими умовами вільного руху системи. Якщо система в рівновазі, то всі похідні вихідної величини х дорівнюють нулю. Точки, що відповідають стану рівноваги, називаються особливими точками. Сукупність фазових траєкторій для всіх можливих початкових умов разом з особливими точками називаються фазовим портретом системи. Якщо лінійна частина описується диференційним рівнянням не вище другого порядку, то фазовий портрет буде зображений на фазовій площині. Часто можна апроксимувати лінійну частину високого порядку рівнянням другого порядку з еквівалентним запізненням. При зображенні процесів на фазовій площині рівняння 2-го порядку заміняють еквівалентним рівнянням 1-го порядку:

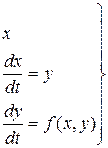(1)

Щоб зобразити (1) на фазовій площині, необхідно виключити час діленням цих рівнянь:

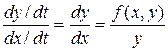(2)

Після розв’язання нелінійного диференційного рівняння (2) отримаємо рівняння фазової траєкторії 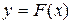(3), що визначає криву на фазовій площині. Кожній сукупності початкових умов 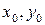відповідають свої розв’язки (3) і своя фазова траєкторія.

Інтегрування (2) можна здійснити аналітично, графічно та чисельно.

Фазові траєкторії, що визначаються (2), мають такі властивості:

1) при у > 0 х завжди збільшується;

2) при у < 0 х завжди зменшується;

3) при збільшенні часу зображувана точка проходить зліва направо у верхній напівплощині і справа наліво у лівій напівплощині;

4) при у = 0, 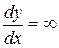, тому в точках перетину фазових траєкторій із віссю х дотичні до них перпендикулярні до осі х.

Якщо (2) важко проінтегрувати, то фазові траєкторії будують за методом ізоклін.

Ізокліна – геометричне місце всіх точок фазової площини х; у, для яких нахил фазової траєкторії дорівнює постійному значенню С_і (криві рівного нахилу).

Наприклад, якщ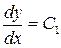о , то 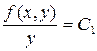, із якого рівняння ізокліни бу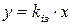де: , де 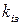– кутовий коефіцієнт ізокліни.

Для кожної ізокліни відомий нахил інтегральної кривої, тому потрібно лише визначити графічно дотичні до інтегральних кривих, а потім і самі інтегральні криві.

Задавшись С_і, будуємо сімейство ізоклін, кожна із яких має 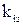для даної САК.

х – вихідна величина;

.

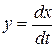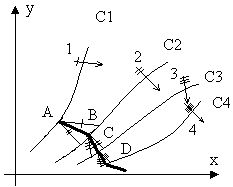
Рис. 1. Ізокліни С1, С2, С3, С4

(1,2,3,4 – дотичні до ізоклін, ABCD – фазова траєкторія)

Нехай побудовані ізокліни для різних значень 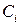і показані нахили дотичних до траєкторій, що перетинають дані прямі. Нехай початкові умови задані точкою А. Тоді з неї проводять дві прямі, паралельні нахилу С1 та С2 до перетину з ізокліною С2. Середина відрізка на С2 між цими прямими є точка В. Аналогічно визначають точки C, D і т.д. З’єднуючи ці точки, отримують криву, що називається фазовою траєкторією.

Методом фазової площини можна користуватися як для нелінійних, так і для лінійних систем.

Приклад. Використання методу фазової площини для дослідження лінійних систем.

Нехай система описується диференційним рівнянням другого порядку (коливальна система).

.

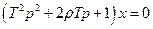Поділемо на 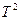, тоді

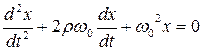; (1)

де 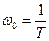– частота власних коливань; 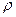– коефіцієнт демпфірування (декремент затухання)

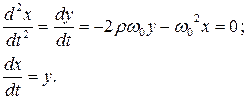(2)

Запишемо фазову траєкторію

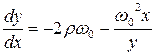. (3)

Після інтегрування (3) одержимо рівняння фазової траєкторії з урахуванням початкових умов. Її вигляд залежить від параметрів r і w₀. Наприклад, при r = 0 (ланка консервативна):

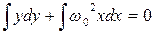(4)

або .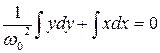

Після інтегрування:

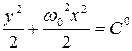або .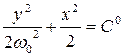

Розділивши на 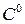і прирівнявши 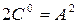, отримаємо рівняння еліпса:

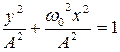або ;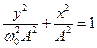

Еліпси визначають фазові траєкторії (криві 1) незатухаючих коливань (рис.2,а), що відповідають наявності пари чисто уявних коренів у рівнянні (1), якщо r = 0.

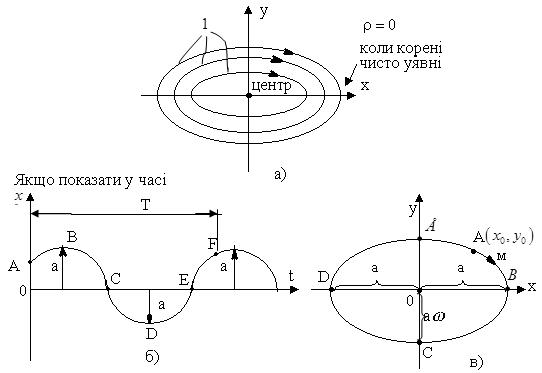Рис.2

Покажемо, який вигляд на фазовій площині мають основні типи процесів керування.

1. Якщо 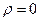, то періодичні коливання будуть з постійною частотою 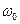й амплітудою а. Нехай процес x(t) починається у точці А з додатним початковим відхиленням х₀ і додатною початковою швидкістю 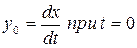. Тоді початкова точка А процесу x(t) буде зображена на фазовій площині (х;у) у вигляді точки М_А з додатними координатами х₀,у₀.

Далі на ділянці процесу АВ (рис.2,б) відхилення х збільшується, а швидкість 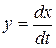зменшується. Відповідно зображуюча точка М на фазовій площині буде рухатися, описуючи криву М_АМ_В. Крива називається фазовою траєкторією. Точка М_В, у = 0 і х = х _макс, відповідає верхній точці В процесу x(t).

Потім ділянці ВС відповідає крива М_ВМ_С. У точці М_С, х = 0, а 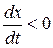. Аналогічно ділянки CD та DE процесу х (t) відповідають руху точки М по кривій М_С М_D М_Е, через час, рівний періоду коливань Т у точці F. САК буде мати ті ж значення відхилень х і швидкості 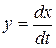, що й з початку процесу. Далі процес періодично повторюється.

Таким чином, будь-який коливальний процес із постійною амплітудою і частотою завжди зображується на фазовій площині у вигляді замкнутого контуру фазової траєкторії. За кожний період точка проходить весь контур.

Якщо коливання х (t) синусоїдальні x = a sin wt, то 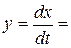aw cos wt. Ці дві формули дають на фазовій площині еліпс із напівосями а (по осі х) та аw (по осі у). Якщо коливання не синусоїдальні, то замкнутий контур на фазовій площині буде відрізнятися від еліпса.

Висновки. Будь-який періодичний коливальний процес з постійною амплітудою і частотою завжди зображається на фазовій площині у вигляді деякого замкнутого контура – замкнутої фазової траєкторії. Кожному періоду коливань відповідає проходження зображуючою точкою всього контура, наприклад, якщо 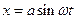, 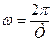де 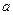– амплітуда, 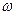– частота 1/с; – одне повне коливання в секунду, то 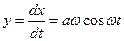тобто еліпс на фазовій площині.

Якщ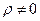о , то

2. Корені комплексні з від’ємною дійсною частиною (тобто процес затухаючий)

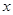
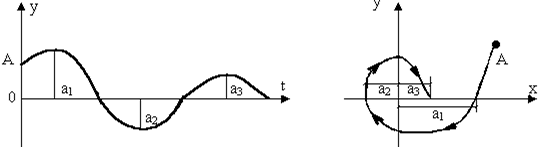
Рис.3. Процес сходиться – САК стійка

3. Корені комплексні з додатною дійсною частиною

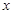
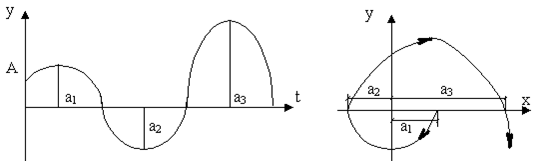
Рис.4. Процес розходиться – САК нестійка

4. Корені дійсні від’ємні (процес аперіодичний)

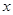
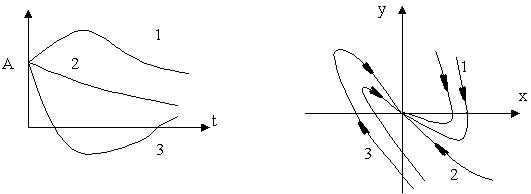
Рис.5. САК стійка

5. Корені дійсні додатні (процес аперіодичний нестійкій)

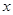
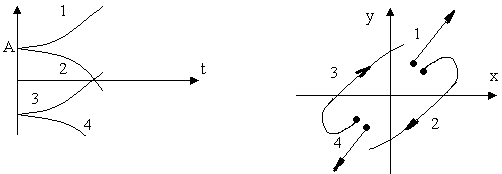
Рис.6. САК нестійка

Дата добавления: 2014-01-04