Лекція №14. Визначений інтеграл

1. Задача про площу криволінійної трапеції. Означення та умови існування визначеного інтеграла

2. Властивості визначеного інтеграла

3. Формула Ньютона-Лейбніца. Методи обчислення визначених інтегралів

4. Застосування визначеного інтеграла

1. Задача про площу криволінійної трапеції. Означення та умови існування визначеного інтеграла

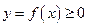Нехай на відрізку задано функцію . Фігура, обмежена графіком даної функції і відрізками прямих 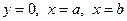, називається криволінійною трапецією. Обчислимо площу цієї трапеції.

Розіб’ємо відрізок 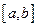на 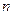довільних частин точками:

.

Сукупність точок 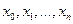позначимо через Т і назвемо Т–розбиттям відрізка .

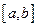На кожному частинному відрізку 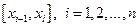, візьмемо довільну точку 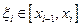і обчислимо значення 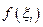. Тоді добуток 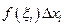, де 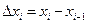- довжина відрізка 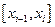дорівнює площі прямокутника з основою і висотою 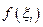, а сума цих добутків 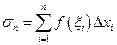(1) – площа ступінчатої фігури і наближено дорівнює площі криволінійної трапеції:

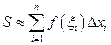. (2)

Сума (1) називається інтегральною сумою функції 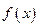, яка відповідає
Т-розбиттю відрізка 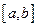на частинні відрізки і даному вибору точок .

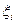Із зменшенням усіх величин точність формули (2) збільшується, тому природно за площу криволінійної трапеції вважати границю площ ступінчатих фігур за умови, що максимальна довжина частинних відрізків прямує до нуля:

.

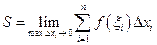Якщо існує скінченна границя інтегральної суми (1) при 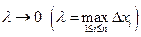, яка не залежить ні від Т–розбиття, ні від вибору точок 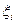, то ця границя називається визначеним інтегралом функції 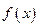на відрізку 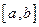і позначається символом .

Отже, згідно з означенням: .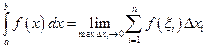

Функція 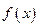називається інтегрованою на відрізку 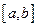. Числа 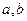називаються відповідно нижньою і верхньою межею інтегрування; функція 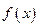називається підінтегральною функцією; – підінтегральним виразом; 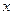– змінною інтегрування; 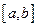– проміжком інтегрування.

Площа криволінійної трапеції, обмеженої прямими 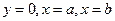і графіком функції 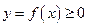, дорівнює визначеному інтегралу від цієї функції 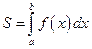. У цьому полягає геометричний зміст визначеного інтеграла: визначений інтеграл від невід’ємної функції чисельно дорівнює площі відповідної криволінійної трапеції.

Умови інтегрованості функцій:

Теорема 1 (необхідна умова інтегровності)

Якщо функція 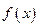інтегровна на відрізку 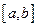, то вона обмежена на цьому відрізку.

Теорема 2 (достатня умова інтегровності)

Якщо функція 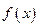неперервна на відрізку 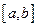, то вона інтегровна на цьому відрізку.

Дата добавления: 2014-01-04