Логические союзы

Высказывания могут быть простыми, когда оно представлено в единственном числе, как какая-то одна мысль, и сложным, когда мыслей несколько и они связаны друг с другом. Сложное высказывание представляет собой соединение простых высказываний с помощью логических союзов. Грамматически такое высказывание выражается сложным предложением.

Простое высказывание рассматривается как нечто неделимое, не разложимое целое. Символически оно обычно обозначается латинскими буквами p, q, r,... и т.д. В данном случае мы отвлекается от того, что простое предложение, понимаемое как мысль, как суждение, состоит из множества структурных элементов (предмет мысли, его свойства и т.п.).

Таким образом, высказывание становится абстрактным объектом, имеющим одно из логических значений – истина или ложь. Такое понимание высказываний позволило использовать по отношению к ним методы функционального анализа, а именно вся совокупность высказываний стала рассматриваться как множество особого рода, состоящая только из двух видов элементов – истинных и ложных, с определенными логическими функциями, представляющими собой операции над этими абстрактными объектами. При этом всегда надо помнить, что логические союзы как функции этих абстрактных объектов имеют единственное строго определенное значение, тогда как грамматические союзы могут иметь различные значения.

Рассмотрим основные логические союзы.

Отрицание ùp .

Точный смысл логических союзов устанавливается с функциональной точки зрения в таблицах истинности. Таблица истинности такого союза является его самой существенной логической характеристикой и определением. Отрицание ùp задаётся таблицей:

p	ùp
И	Л
Л	И

Первый столбец таблицы называется входным. В нем отмечены все возможные логические значения простого высказывания, например, р. Во втором столбце, который называется выходным, отмечено соответствующие логическое значение отрицания этого высказывания р.

Отрицание – это логический союз, позволяющий производить логическую операцию, с помощью которой образуется новое сложное высказывание, истинное тогда и только тогда, когда исходное высказывание ложно, и ложное, когда исходное высказывание истинно. Таким образом, при отрицании высказывание р получают высказывание, значение истинности которого противоположно значению истинности р.

Если отрицается высказывание р, то получается высказывание ùp. Это последнее выражение читается: “неверно, что р ”, или “ложно, что р ”, или просто “не- р ”. Если отрицается сложное высказывание, то перед выражение ставится знак ù. Выражение 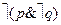читается так: “неверно, что р и не- q ”.

Возможные ошибки при употреблении отрицания

· В живой речи отрицание выражается различными способами. Приведем пример: “неверно, что эта книга интересная”. В логике речевой оборот “Неверно, что…” употребляется как языковое выражение для отрицания высказывания и, стало быть понимать его следует только так. Допустим, мы скажем: “Эта книга не интересная”. Оба повествовательных предложения практически равнозначны, они подразумевают одно и то же. Однако во второй формулировке отрицается не высказывание, а только понятие, составляющее часть содержания высказывания. Поскольку высказывания представляет собой единое неделимое целое, то и отрицать его можно только целиком. Если это требование не выполняется, то происходит произвольная замена одного высказывания другим.

Проанализируем пример с такого рода ошибкой. Пусть принимается за отрицание высказывание “Все розы не красные”, тогда получится высказывание “Все розы - красные”. Первое высказывание ложно, поскольку имеются розы красного цвета, если бы второе высказывание было отрицанием первого, то оно было бы истинным. Но оно также ложно, поскольку в нем утверждается, что вообще нет роз другого цвета кроме красного. По правилу отрицания мы обязаны сказать, что отрицаем высказывания “Все розы не красные” является только высказывание “Неверно, что все розы не красные”.

· Следует различать логическое и диалектическое отрицания. Такое различие становится очевидным в случае с двойным отрицанием. В логике дважды отрицаемое высказывание имеет то же значение истинности, что и соответствующее высказывание, не содержащее отрицаний, и может быть заменено им. Двойное диалектическое отрицание – отрицание отрицания – выражает поступательный характер развития. Это третья ступень развития, которая противоположна второй ступени и в каких-то чертах сходна с первой, но находится на более высоком и сложном уровне.

Конъюнкция (&).

Конъюнктивными называются сложные высказывания, образованные из простых при помощи соединения их логическим союзом “и”.
В речи конъюнкция может выражаться различными словами, такими, например, как “и”, “а”, “но”, “да”, “хотя” “который”, “зато”, “однако”, “не только,... но и …”, “как …, так и …” и др., в письменном варианте – знаками препинания: запятой, точкой с запятой, тире. Приведем ряд примеров: “Шел снег, и было холодно”. “Ель растет перед дворцом, а под ней хрустальный дом” (Пушкин).

p	q	p&q
И	И	И
И	Л	Л
Л	И	Л
Л	Л	Л

Пусть даны два произвольных высказывания p и q, соединенных конъюнктивно. Построим таблицу, которая содержит все возможные комбинации их логических значений. Число распределений истинности и ложности таких высказываний требует уже двух входных столбцов и четырех строчек. Во входных столбцах будем придерживаться строгой последовательности переборе значений по строкам. В выходном столбце получим те значения истинности, которая принимает конъюнкция в зависимости от распределения истинности и ложности исходных простых высказываний. При этом p и q будем называть конъюнктивными членами или просто конъюнктами. Символически конъюнкция обозначается знаком “&” или “”.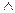

Таблицу истинности для конъюнкции можно проиллюстрировать ситуацией “свидание”:

1-я строка – Он пришел на свидание (p истинно), и она пришла (q истинно). Свидание состоялось. Высказывания p и q оба вместе истинны. 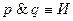. Знак “” читается “равносильно” и означает “то же самое, что и…”.
2-я строка – Он пришел на свидание (p истинно), но она не пришла (q ложно). Свидание не состоялось. Высказывания p &ù q оба вместе ложны. .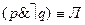
3-я строка – Он на свидание не пришел (p ложно), а она пришла (q истинно). Свидания нет. Высказывания ù p & q оба вместе ложны. .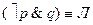
4-я строка – Ни он, ни она на свидание не пришли. .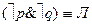

Дата добавления: 2014-01-04