Синтаксис логики высказываний

Синтаксическое описание системы классической логики состоит из трёх исходных типов символов (элементарных знаков), составляющих алфавит языка логики высказываний, и правил образования правильных выражений этого языка.

Алфавит – совокупность исходных символов данного формализованного языка:

1. нелогические символы представляют собой простые высказывания, выражаются буквами p, q, r, s, p1, …;

2. логические символы, к которым относятся логические союзы и знак отрицания: &, Ú, ,É, º, ù;

3. технические символы: (,), т.е. левая и правая скобки.

С помощью данных символов строятся выражения языка логики высказываний.

Формула является тождественно истинной, если она истинна при любых значениях входящих в неё переменных. Формула называется противоречием, если она ложна при любых значениях входящих в нее переменных. Две формулы алгебры логики A и B называются равносильными, если они принимают одинаковые логические значения при любом наборе значений входящих в формулы элементарных высказываний (переменных). Обозначение A≡B.

Таблица основных равносильностей

Законы коммутативности:

1. ,

2. .

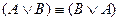Законы ассоциативности:

3. ,

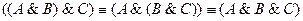4. .

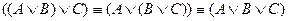Законы дистрибутивности:

5. ,

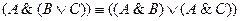6. .

Законы поглощения:

7. ,

8. .

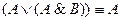Законы идемпотентности:

9. ,

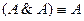10. .

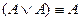Законы отбрасывания:

11. 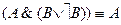- закон исключения тавтологии из конъюнкции,

12. - закон исключения противоречия из дизъюнкции.

Правила упрощения:

13. ,

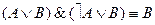14. .

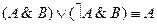Правила зачеркивания посылки:

15. ,

16. .

Правила выявления:

17. ,

18. .

Правила, вытекающие из табличных определений конъюнкции и дизъюнкции:

19. ,

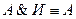20. ,

21. ,

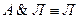22. .

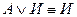Законы де Моргана:

23. ,

24. .

Закон двойного отрицания:

25. .

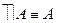Лекция №3 “Понятие”

План лекции:

1. Понятие как форма мышления и вид мысли

2. Предмет, имя, понятие; их соотношения

3. Признаки и их виды

4. Языковые и логические формы выражения понятий.

5. Логическая структура и основные характеристики понятия

6. Виды понятий

Дата добавления: 2014-01-04