Отношений между понятиями

Диаграммы Венна как прием анализа

Способ представления объемов понятий на кругах Эйлера оказался малопригодным в тех случаях, когда не ясен объем понятия. В частности, если понятие является не простым, а сложным, то возникают неопределенности. Английский логик Джон Венн (1834 - 1923) {главный труд ”Символическая логика” (1991), заметим, что термин “символическая” был применен к логике здесь впервые} разработал графический аппарат диаграмм, с помощью которого выявляются отношения между объемами практически любых понятий. Алгебра Буля здесь получила дальнейшую оригинальную разработку, логика классов стала эквивалентом исчисления первопорядковой логики предикатов.

Например, имеется такое понятие: x (P(x) & ( ך Q(x) V R (x))). Пусть это понятие пробегает по универсуму U. Рассмотрим три способа разделения плоскости универсума на фигуры. Рисуем квадрат (круг), символизирующий этот универсум.

Далее разбиваем его плоскость на 2ⁿ прямоугольников, где n – число предикаторов, заданных в анализируемом понятии. В приведенном понятии есть три предикатора P,Q и R. Разделим имеющийся универсум по каждому предикатору пополам в такой последовательности: вертикальной чертой для первого предикатора (справа рисуем известные нам круговые схемы и их графические аналоги из логики классов).

Одна его часть (P) означает принадлежность свойства P предметам “x”. Другая его часть ( ך P) означает: “Неверно, что предметы “x” данного универсума обладают свойством P ”. Обратим внимание на то, что приемом разбиения плоскости надвое осуществляется дополнение одного класса до универсума.

Горизонтальной чертой выделим плоскости для второго предикатора.

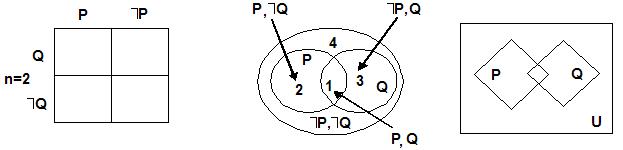
Для третьего предикатора вновь используем вертикальную черту дважды для разбиения плоскостей P и ך P. При n = 3 универсум разбивается на 8 областей.

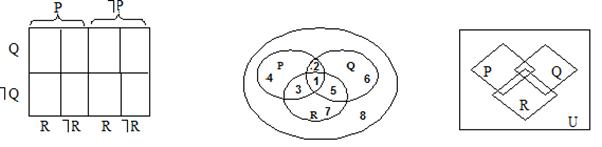
В круговой схеме плоскости означают: 1 – P Q R, 2 – P Q ך R, 3 – ך P Q R, 4 – P ך Q ך R, 5 – ך P Q R, 6 – ך P Q ך R, 7 – ך P ך Q R и 8 – ך P ך Q ך R. Графическая схема имеет соответствующие 8 областей.

Если бы имелся четвертый предикатор, например S, то плоскости Q и ך Q делились бы еще горизонтальными чертами с тем, чтобы получить плоскости для S и ך S.

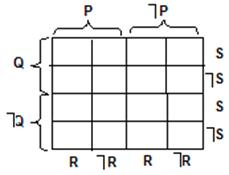Для четырех предикаторов получили 16 малых квадратов, то есть перебор всех их возможных комбинаций. Черта, разбивающая квадрат, не принадлежит ни к одному из получившихся прямоугольников символизирующих объем какого-либо из предикаторов. Исходной позицией диаграммы в графическом изображении служит взаимное пересечение классов. Каждый прямоугольник диаграммы нумеруется. При n = 4 возможны такие варианты изображения в круговых схемах и графической схемы для логики классов:

    U 15 D C 14 13 11 B 6 9 A 5 1 10 7 2  

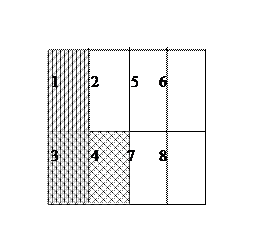Операции осуществляются следующим образом. Отрицанию соответствует дополнение (‘), дизъюнкции соответствует объединение (U), а конъюнкции - пересечение (∩). Каждому xA(x) будет соответствовать свой объем. Теперь на схеме слева штриховкой устанавливаем объем для первого предикатора (P). На средней схеме штрихуем объем для части понятия ( ך Q(x) V R(x)) и, наконец, на схеме справа по совместному списку предикаторов находим объем исходного понятия x(P(x) & ( ך Q(x) V R(x))).

W_x P(x)

Приведем пример: “Город, такой, что он крупный и, если он имеет пристань, то стоит на реке”.

x (крупный (x) и (если x имеет пристань, то x стоит на реке)). Заменим имеющиеся связи на логические союзы. Будем иметь:

x (крупный (x) & (имеет пристань(x) É стоит на реке (x))):

Теперь запишем термины данного выражения символами языка логики предикатов и заменим импликацию на дизъюнкция. После такой процедуры получим знакомую формулу:

x (P(x) & ( ך Q(x) V R(x))).

Запишем формулу в объемной интерпретации:

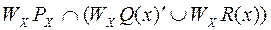
Пронумеруем диаграмму Венна для построенной формулы и запишем полученный результат.

1.	P,	Q,	R	-	P	∩	Q	∩	R
2.	P,	Q,	ךR	-	P	∩	Q	∩	ךR
3.	P,	ךQ,	R	-	P	∩	ךQ	∩	R
4.	P,	ךQ,	ךR	-	P	∩	ךQ	∩	ךR
5.	ךP,	Q,	R	-	ךP	∩	Q	∩	R
6.	ךP,	Q,	ךR	-	ךP	∩	Q	∩	ךR
7.	ךP,	ךQ,	R	-	ךP	∩	ךQ	∩	R
8.	ךP,	ךQ,	ךR	-	ךP	∩	ךQ	∩	ךR

Разбиваем универсум на 8 частей и находим объем для Р (первая диаграмма). На второй диаграмме производим операцию объединения для ך P(х) V Q(x). Теперь по совместному списку предикаторов находим объем исходного понятия. Для этого осуществим пресечение полученных классов (диаграмма 3). Только объем области, записанной на первой строке и обозначенной на диаграмме цифрой 1, соответствует объему анализируемого понятия. Вторая область пуста, поскольку это город, который не стоит на реке, но пристань имеет. Третья область отображает город, такой, что он стоит на реке, но пристани не имеет. Первая и третья области находятся в отношении соподчинения с городом, стоящем на реке, в отношении пересечения с крупным городом, не имеющим пристани. Четвертая область интересна тем, что соответствует крупному городу не стоящему на реке и не имеющему пристани. Области 5, 6, 7 и 8 пусты, так как не относятся к крупному городу и находятся к нему в отношении совместимости.

Деление Понятий.

Практическая и научная деятельность приводит к необходимости группировать явления действительности, выявлять их виды и классы. При этом приходится устанавливать тот круг объектов, который мы отображаем в том или ином понятии. Такая логическая операция, направленная на отыскание объемов понятий, называется операцией деления понятий.

Логическая операция, раскрывающая объем понятия путем перечисления его видов, называется делением (от лат. divisio-деление, разделение на отдельные группы) понятия. Или просто, разделить понятие – значит раскрыть его объем.

В делении будем различать следующие компоненты:

1) делимое (лат. totum dividendum-делимое понятие) – это понятие, объем которого подвергается делению;

2) члены деления (лат. membra divisionis-члены деления) – это видовые понятия, получающиеся в результате деления;

3) основание деления (лат. fundamentum divisionis-основание деления, или principium divisionis-принцип деления) – это признак, с учетом которого производится деление.

Суть этой операции состоит в разделении понятия на составляющие его виды. Пусть например, делимым понятием будет понятие «вещество». Разделить объем этого понятия означает найти его видовые понятия, скажем «простое вещество» и «сложное вещество». xA(x) – делимое понятие. xB₁(x), xB₂(x),…, xB_n(x) – члены деления. Деление – это такая логическая операция, в которой общее (родовое) и особенное (видовое), как две стороны каждой вещи, находят свое раздельное проявление – находясь в соподчинении между собой, видовые понятия подчиняются общему для них роду. Основание деления – это такой признак, который позволяет перейти от исходного понятия к членам деления. В зависимости от этого признака различают два вида или приема деления: по видоизменению признака и дихотомическое (деление понятия на два вида).

Дата добавления: 2014-01-04