
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Отношения между объемами простых понятий
|
|
|
|
В объективном мире взаимная зависимость вещей и явлений, их обусловленность друг другом носит всеобщий и универсальный характер. У каждой отдельной вещи существует бесконечное многообразие связей с другими вещами, с миром как целым. Признание положения о том, что в мире каждая вещь связана с каждой, присуще любой логически последовательной философии. Понятия, будучи отражением действительности, также вступают в различные связи и отношения друг с другом.
Всякая связь включает в себя как свой момент обособленность. Обособленность – это сохранение типа связи и относительной независимости конкретной вещи от другой вещи. Абсолютно обособленных, изолированных вещей нет. Обособленность существует только как относительная. Так, если вещи нетождественны в каком-либо отношении, то между ними нет и соответствующей связи, то есть существует обособленность этих вещей в данном отношении. Наличие отношений между вещами дает возможность выделять и абстрагировать в познании определенные связи.
Исследование связи с позиции движения и развития позволило раскрыть ее природу как взаимодействие. Вещи не просто связаны между собой, они взаимодействуют друг с другом, образуя тем самым единое целое – объективный мир. Взаимодействие характеризует связь прежде всего как процесс, как способ связи (обмен содержанием, направленность движения и т.д.). Взаимодействие, таким образом, отражает тот факт, что в универсальной связи вещей и явлений противоположности сходятся и переплетаются друг с другом, меняются местами.
Понятие связи раскрывается далее через понятие «взаимосвязи» и «зависимости». Термин «взаимосвязь» употребляется в широком смысле для обозначения прямых и опосредованных связей («все в мире взаимосвязано»). В своем специфическом значении термин «взаимосвязь» обозначает взаимное изменение вещей, указывает на двусторонний характер связи.
Термин «зависимость» («взаимозависимость») является наиболее глубокой характеристикой сущности связи. В понятии «зависимость» важнейшим является признак подчинения связанных между собой вещей, определенной направленности действия. Здесь следует различать два момента: зависимость вещи от других вещей и зависимость вещи от самой себя. Поскольку данная вещь зависит от других вещей и определяется ими (в своем возникновении, существовании и исчезновении) – она относительная. Поскольку данная вещь возникла как таковая, как эта вещь, постольку она определяется прежде всего самой собою. Соотношение с собой означает безотносительность к другому, самостоятельность, абсолютность вещи. Вещи, которые были бы абсолютными во всех отношениях, ни от чего независимыми, у которых природа ни в какой мере не опосредовалась бы другими вещами, не существует. Но нет и таких вещей, природа которых полностью определялась бы только другими вещами.
Связь – одна из важнейших характеристик действительности. Нельзя понять ни одного явления не рассматривая его вне связи с другими, вне их взаимного воздействия, обусловленности друг с другом. Прежде всего мы рассмотрим отношения простейшего вида – прямые и однопорядковые, и лишь после этого прейдем к анализу более сложных, позволяющих одновременно вычленять многообразие связей, присущих понятиям.
Сравнивая два понятия можно установить, что некоторые признаки, мыслимые в их содержании, являются общими для обоих понятий, а некоторые – различными. Так, в понятиях «философ» и «художник» одни признаки в их содержании – общие, а именно, духовное освоение действительности, познание внутреннего мира человека и т.п. Другие признаки в содержании этих понятий – различны, поскольку имеют место особые подходы к действительности, выявляющие иные, относящиеся к другому уровню, другим сторонам, предметы познания. Понятия, в содержании которых имеются как общие, так и отличающиеся друг от друга признаки называются сравнимыми. Из признания всеобщей и универсальной связи вещей и явлений мира следует, что два любых понятия могут быть сравнимыми. Тем не менее, существуют понятия, отражающие разные области действительности с таким далеким друг от друга содержанием, общие признаки которых столь опосредованы, что сравнение и сопоставление таких понятий теряет всякий смысл. Их сравнение не дает приращения зрения, а подчас становится даже бессмысленным. Понятия, в содержании которых нет ни одного, с указанной точки зрения, общего признака, называются несравнимыми. Примерами несравнимых понятий могут служить «гармония» и «зубная боль», «скрипка» и «кирпич» и т.д. Оставим в стороне несравнимые понятия и займемся анализом сравнимых понятий, поскольку именно им принадлежит все богатство связей и отношений.
Сравнимые понятия в практическом отношении всегда ограничиваются определенным общим для них универсумом рассуждения. Это обстоятельство подчас приобретает принципиальное значение и возникает вопрос о правомерности сравнения понятий. Так, сравнение понятий, принадлежащих к различным философским направлениям, школам, концепциям нуждается в соответствующем обосновании.
По характеру логических отношений сравниваемые понятия разделяют на совместимые и несовместимые. Совместимыми называются понятия, объемы которых совпадают полностью или частично. Так, понятия «философ» и «поэт» - совместимые понятия. Их содержание не одно и тоже, оно состоит из разных признаков. Но это различие не таково, чтобы исключалась возможность таких философов, которые одновременно были бы еще и поэтами, и таких поэтов, которые вместе с тем были бы и философами. Таковыми, например, были Эмпедокл и Петрарка, Лукреций Кар и Гете.
Совместимость понятий выражается в трех видах отношений между ними: равнообъемности, пересечения и подчинения. Равнообъемными называются понятия, имеющими один и тот же объем, но различное содержание. Например, «самая большая река в Европе» и «великая русская река». Отражая разные признаки одного и того же предмета эти понятия имеют различное содержание, но объемы их полностью совпадают, так как мыслится один и тот же предмет. С семантической точки зрения наглядным изображением, поясняющим отношения между простыми понятиями, служат круговые схемы Эйлера. Круг как часть плоскости ограниченной окружностью произвольного, но фиксированного радиуса символизирует собой класс предметов, составляющих объем понятия, а каждая точка внутри круга – элемент этого объема. Отношение между равнообъемными понятиями изображается совмещенными друг с другом кругами одного и того же радиуса. Так, если символом А обозначим понятие «отец логики», а символом В обозначим понятие «автор «Органона»», то объемы этих понятий совпадают и изображены на схеме совмещенными друг с другом кругами.

Из различия содержаний таких понятий вытекает, что из знания об одном не следует с необходимостью знание о другом, поскольку они характеризуют одну и ту же вещь или явление с разных сторон. В связи с равнообъемностью понятий существует проблема интерпретации имен как их словесного (знакового) закрепления в плане синонимии (слов, различных по звучанию, но тождественных по значению, когда за одним и тем же понятием установилось разное терминологическое закрепление; скажем, «континент» как латинское слово и «материк» как собственно русское служат для выражения одного понятия) и омонимии (слов, различных по значению, но тождественных по звучанию, скажем, за одним и тем же термином «свобода» в различных философских, идеологических и т.д. позициях закреплены разные понятия). Попутно заметим, что два несравнимых понятия, при необходимости, могут быть представлены двумя изолированными кругами.
Вторым видом отношений совместимых понятий является пересечение. Пересекающимися называются понятия, содержание которых различно, но объемы их частично совпадают. Это означает, что предмет, принадлежащий объему одного из таких понятий, одновременно принадлежит объему и другого. Например, «философ» и «математик» - пересекающиеся понятия. Их содержание различно, но часть объема одного является общей частью объема другого. Не все философы – математики, и не все математики – философы, но есть среди философов математики и среди математиков – философы. Отношение пересечения наглядно изображается частично совмещающимися кругами:


Предельным случаем такого пересечения является ситуация, при которой общая для объема обоих пересекающихся понятий часть представлена единственным предметом. Примером такого случая могут служить понятия «выдающийся философ» и «великий художник». Это – Леонардо да Винчи.
Третьим видом совместимых понятий являются понятия, вступающие в отношение подчинения. В данном отношении находятся такие понятия, объем одного из которых полностью входит в объем другого, но не исчерпывает его. Понятие с большим объемом называется подчиняющим, а понятие с меньшим объемом – подчиненным. Отношение подчинения можно проиллюстрировать следующей схемой.

 |
Отношение подчинения изображается двумя кругами, один из которых расположен внутри другого. В отношении подчинения находятся, например, понятия «университет» (А) и «высшее учебное заведение» (В).
Отношение подчинения могут быть между двумя общими понятиями, тогда подчиняющее понятие называется родовым, а подчиненное – видовым. В отношении подчинения могут находиться общие и единичные понятия, тогда первое выступает как видовое по отношению ко второму как индивиду. Логическое отношение подчинения может иметь в пределе тот случай, когда оба понятия становятся эквивалентными и их объемы совпадают. Следовательно, равнообъемность становится предельным случаем подчинения при условии нестрогого включения. Такой тип подчинения может иметь место в некоторых определениях.
Отношение подчинения – самый существенный вид логических отношений между понятиями, оно чаще всего встречается в практике научного мышления. При оперировании подчиняющими и подчиненными понятиями может возникнуть логическая ошибка, когда часть целого рассматривается как видовое понятие. Проверкой служит здесь подведение такого видового понятия под признак рода. Если имеет место логическая ошибка, то при такой проверке она становится очевидной.
Обратимся к несовместимым понятиям. Несовместимыми называются понятия, объемы которых не содержат в себе общих элементов. Содержания таких понятий составляют признаки, которые не могут одновременно принадлежать одному и тому же предмету и, следовательно, исключают возможность даже частичного совпадения их объемов. Например, «добро» и «зло», «печаль» и «радость» и т.п. Несовместимые понятия могут вступать в отношения соподчинения, противоположности и противоречия. Объемы таких понятий находятся в строго дизъюнктивном или эксклюзивном отношении.
Отношение соподчинения являются разновидностью родовидовых отношений. Объемы соподчиненных понятий составляют самостоятельные, не совпадающие друг с другом виды родового понятия, и которые в равной мере подчинены этому родовому понятию. Кратчайшим образом, соподчиненными называются виды одного и того же рода. Например, «поэзия» и «архитектура» являются понятиями, подчиненными одному родовому для них понятию «искусство». Отношение соподчинения наглядно можно изобразить в виде круговой схемы:

 |  |
При этом родовое понятие называется подчиняющим, а видовые – с оподчиненными. При оперировании соподчиненными понятиями надо иметь в виду два правила несовместимости. Первое правило: соподчиненные понятия должны быть ближайшими видами одного общего для них рода. Несоблюдение данного правила приводит к ошибке соподчинения видовых понятий, принадлежащих разным родовым понятиям. Второе правило: соподчиненные понятия не должны находится в отношении пересечения.
Вторым видом отношений между несовместимыми понятиями является отношение противоположности. Два соподчиненных понятия называются противоположными (контрарными), если одно из них содержит такие признаки, которые исключает другое понятие, замещая их на противоположные. Имена таких понятий выражаются в языке антонимами. Например, «тяжелое» и «легкое», «далекое» и «близкое» и т.п. Отношение противоположности присуще таким видовым понятиям, которые находятся на крайних полюсах рода. Иллюстрацией такого положения может служить схема:



Оба противоположных понятия «белое» (В) и «черное» (С) входят в объем подчиняющего понятия «цвет» (А), но полностью всего объема подчиняющего понятия не исчерпывают. Между противоположными понятиями существуют промежуточные виды со своими признаками. Между крайними противоположностями белого и черного цветов можно последовательно перечисляя объем средний части перейти от одного к другому, и наоборот.
Третьим видом отношений между несовместимыми понятиями является отношение противоречия. Противоречащими (контрадикторными) называются соподчиненные понятия, которые исключают друг друга и оба вместе полностью исчерпывают объем родового понятия. Отношение противоречия графически изображается так:


Например, «белый» и «небелый». В отношении противоречия находятся положительные и отрицательные понятия. Оба эти понятия одновременно и в одном отношении нельзя применить к одному и тому же предмету не впадая в логическое противоречие. Древнегреческий поэт Феогнид из Мегар (VI в. до н.э.) подвел безрадостный итог совей жизни в такой контрадикторно сформулированной сентенции:
«Сделав, я не сделал и не закончил, закончив;
совершив, не совершил и достигнул, не достигнув».[1]
Для того, чтобы отличить противоположные и противоречащие понятия, следует придерживаться двух правил: 1) противоречащие – это пара понятий, одно из которых положительное, а другое – отрицательное; противоположные понятия оба положительны; 2) противоречащие понятия оба вместе исчерпывают класс предметов, мыслимых в понятии; противоположные – не исчерпывают весь объем родового понятия.
Отношение противоречия и противоположности выполняют особую роль в логическом рассуждении. Каждое из них может достигать такой интенсивности и такого утончения, когда одно превращается в другое. Полемика об этих понятиях до сих пор не приводит к полному удовлетворению.
В ряду противоположных понятий есть такие, которые находятся в отношении бинарной оппозиции (лат. оppositio – противопоставление). Существуют три вида бинарной оппозиции. 1) Прямое противопоставление, при котором два понятия контрарны по содержанию, то есть оба являются положительными, но в своей совокупности исчерпывают весь объем родового понятия. Между содержаниями таких понятий имеет место двусторонняя импликация. Например, «правый» и «левый», «верх» и «низ», «восток» и «запад», «плюс» и «минус», «истина» и «ложь» и т.п. Один выступает антиподом другого. 2) Косвенное противопоставление (ослабленная оппозиция), при котором два понятия контрадикторны по содержанию, то есть одно из них положительное, а другое – отрицательное, но в своей совокупности они не исчерпывают всего объема родового понятия. Между содержаниями таких понятий возможна только односторонняя импликация. Например, «старый» и «нестарый». Между такими понятиями существуют промежуточные виды («зрелый», «пожилой» и т.п.). Из содержания одного («старый») не следует содержание другого («молодой»). Пример амбивалентного отношения: «любовь – ненависть». 3) Конверсная оппозиция, при которой фиксируется контраст сравниваемых понятий (оба положительные), их резкое противопоставление. Например, «лед» и «пламя», «умный» и «дурак» и т.п.[2]
В свою очередь бывает, хотя и редко, ситуация, при которой соподчиненные понятия исчерпывают весь объем родового понятия и при этом не являются противоречащими. Например, «простое предложение» и «сложное предложение». Они исчерпывают все виды предложений, выделенных с указанной точки зрения.
Анализ круговых схем показывает, что попытка выдержать требование выявления отношений между двумя произвольно взятыми сравнимыми понятиями наталкивается на ряд серьезных затруднений и, прежде всего на ситуацию, принуждающую вводить третье понятие, без которого вид отношения между двумя понятиями не может быть установлен. Так, обсуждение двух соподчиненных понятий обнаруживает, что отношение соподчинения принуждает мыслить еще одно (третье) понятие, подчиняющее каждое из них. В противном случае отношение соподчинения исчезает. На круговых схемах они принимают вид несравнимых понятий, но это противоречит их смыслу, поскольку они являются ближайшими видами своего родового понятия. Данное обстоятельство приводит к необходимости введения отношения подчинения, которое, в свою очередь, не присущее несовместимым понятиям. К тому же ряд отношений между понятиями в круговых схемах просто невыразимы. Еще раз подчеркнем, что для выявления отношений между понятиями были приняты условия: 1) выявляются и анализируются отношения, присущее двум совместимым понятиям (осуществляется по парный анализ понятий); 2) для ясности и определенности возможных отношений рассматриваются только простые понятия.
Осуществим второй семантический подход для интерпретации и наглядного представления отношений между простыми понятиями, который задается модельными схемами, является их полным перечнем и снимает ряд затруднений, встречающихся в круговых схемах Эйлера. Такие модельные схемы были предложены Кейнсом в 1906 году.
Предположим, даны два понятия x A (x) и x B (x) и пусть родом первого понятия будет U, а второго U2. Если универсумы U и U2 различны и в них нет ни одного совпадающего элемента, то они являются несравнимыми. Так, если два понятия, одно из которых x А (х), скажем "мудрость" принадлежит универсуму U, а второе - x B (x), например, «голубизна», относится к универсуму U2, то объединение таких универсумов образует нелепость. В качестве подобных примеров можно привести образование универсумов, представляющих универсумы разного порядка, таких как вещи и ее части, вещи и ее свойства и т.п. Возникновение универсумов такого рода приводит к противоречиям и парадоксам. Стало быть, запрет на объединение несравнимых понятий правомерен из-за возможных противоречий образуемого из них общего универсума. Такого рода универсумы не могут совпадать между собой.
Если роды двух понятий совпадают хотя бы в единственной своей части, то имеют место сравнимые понятия. Именно о таких универсумах и отношениях, в которых могут находиться сравнимые понятия, строится новая семантика. Особенностью данной семантики является допущение пустых универсумов, то есть областей реально несуществующих объектов и, следовательно, понятий, объем которых пуст, непустых универсумов и таких универсумов, когда родовое понятие совпадает с универсумом рассуждения. Получим следующий перечень модельных схем:
| А = Ø В = Ø | А=Ø B= U | А=U B= Ø | A = U B = U |  A = Ø A = Ø
|  В = Ø
В = Ø
|  А = U А = U
|  В = U
В = U
| |||||||||

|  
|  
|  
|  
| А | В | 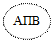 А А
| В | ||||||||
Выделим из числа сравнимых понятий три фундаментальных отношения.
1) Отношение совместимости имеет место тогда и только тогда, когда пересечение объемов понятий х А (х) и х B (х) не являются пустыми:
DWхА(х)∩ WхВ(х)¹Æ
Запись можно упростить так: А∩В ≠ Ø Отношение совместимости означает, что должен существовать хотя бы один предмет, для содержания которого было бы верно $х(А(х)&В(х)). На модельных схемах такому отношению соответствуют 4, 7, 8, 9, 10, 11, 12 и 15 схемы.
2) Отношение исчерпывания имеет место тогда и только тогда, когда объединение понятий х А(х) и хВ(х) совпадает с универсумом:
DWх А(х) U WхВ(х)=U
В упрощенной записи: АUB=U. Содержание понятий, находящихся в отношении исчерпывания "х(А(х) V B(х)) равно универсуму. На модельных схемах такому отношению соответствуют 2, 3, 4, 7, 8, 14 и 15 схемы.
3) Отношение включения имеет место тогда и только тогда, когда одно понятие входит в объем другого понятия. Для двух понятий хА(х) и хВ(х) отношение включения выполняется при условии:
D (WхА(х) ÍWхВ(х)) V (Wх В(х) ÍWхА(х)).
В упрощенной записи будем иметь (АÍВ)V (ВÍА), где "Í" знак нестрогого включения. Для содержания этих понятий достаточно, что х (А(х) ÉВ(х)), либо "х(В(х)ÉА(х)). На модельных схемах такому отношению соответствуют 5, 6, 7, 8, 10 и 11, а так же 1, 2, 3, 4 и 9 схемы как предельные случаи.
Указанные три вида отношений получили название фундаментальных в силу того, что их различные сочетания порождают все другие возможные отношения между двумя сравнимыми понятиями, образуя производные отношения. Из числа таких производных отношений назовем следующие.
1) Отношение несовместимости. Два понятия хА(х) и хВ(х) находятся в отношении несовместимости, если и только если, их пересечение пусто
DWхА(х)∩ WхВ(х)=Ø,
или кратчайшим образом: А∩В= Ø. Их содержания отвечают требованию ┐$х(А(х)& B(х)).
2) Отношение неисчерпывания. Два понятия хА(х) и хВ(х) находятся в данном отношении, если и только если их объединение не образует полного универсума
DWх А (х) U WхВ(х) ≠U,
или кратко: АUВ ≠U. Их содержания удовлетворяют условию: ┐"х(А(х)VВ (х)).
3) Отношение подчинения. Понятия хА(х) и хВ(х) находятся отношении подчинения, если имеет место включения объема одного из них в объем другого. При прямом включении объем второго понятия полностью входит в объем первого понятия. В упрощенной записи это можно указать так (АÍВ). При обратном включении понятие В находится в объеме А: (ВÍА).
Пустое понятие включается в любое другое понятие. Так, если из двух понятий "хА(х) и "хВ(х), хотя бы одно пусто, то его включение может быть записано так:
(WхА(х)= Ø) É(WхА(х) ÍWхВ(х),
или иначе: для всякого В верно, что В(ØÍВ).Аналогично в другом случае.
Если из двух понятий хотя бы одно является универсальным классом, то есть совпадает с униерсумом, то для "х А(х) и "х В (х) будет верно
(Wх А (х) = U) É (Wх В (х) Í Wх А (х)),
или иным способом записи: для всякого В верно, что (В Í U).
Аналогично в другом случае.
Как прямое, так и обратное включение может быть строгим или нестрогим. Отношение строгого включения характеризуется тем, что объем понятия хА(х) строго включается в объем понятия хВ(х), если выполняется условие:
(АÍВ) & ┐(ВÍА),
в кратчайшей записи АÌВ. В этой ситуации хА(х) есть вид, а хВ(х)- род, и где "Ì" -знак отношения строгого включения. В другом случае, при котором второе понятие включено в объем первого, то верным будет условие: (ВÍА).& ┐(АÍВ), или кратко ВÌА, где хВ(х)- видовое понятие, а хА(х)- родовое. Когда, например, понятие хА(х) строго включено в понятие хВ(х), тогда WхА(х)<WхВ(х) и для всякого "х" верно, что если хÎA, то хÎВ. Иными словами, А не совпадает с В, то есть А≠В, и объем А меньше объема В. В этом случае множество А является собственной частью множества В. Аналогично и для другого случая, когда понятие хВ(х) строго включается в понятие хА(х). При нестрогом включении условие А≠В не ставится.
Из названных отношений следует, что возможны четыре вида подчинения:1) совместимые и исчерпывающие - представлены модельными схемами 7 и 8; 2) несовместимые и исчерпывающие - схемы 2 и 3; 3) совместимые и неисчерпывающие - схемы 10 и 11; 4) несовместимые и неисчерпывающие - представлены модельными схемами 5 и 6.
4) Отношение равенства. Понятия хА(х) и хВ(х) находятся в отношении равенства, если объемы их совпадают: (АÍВ) & (ВÍА) при А=В, то есть, такие понятия равнообъемны.
На модельных схемах представлены три вида равенства. В первой модельной схеме А=В и их объемы пусты. Wх А(х)= Ø и Wх В(х) = Ø. На 4-ой модельной схеме воспроизведено равенство для универсальных понятий, когда Wх А(х)=U1 и Wх В(х)= U2, причем так, что U1= U2. Символическим изображением данных отношений являются совмещенные друг с другом прямоугольные четырехугольники. В том и другом случаях имеет место отношение графического равенства. Такие понятия находятся в отношении совместимости и исчерпывания. На 9-ой модельной схеме отображено равенство классов, когда А и В не пусты и не универсальны. Они находятся в отношении совместимости и неисчерпывания.
5) Отношение пересечения. Имеются два вида отношений между пересекающимися понятиями. На 12-й модельной схеме представлено неисчерпывающее и совместимое пересечение. Два понятия хА(х) и хВ(х) находятся в данном отношении, когда правомерно утверждение Wх А(х) U Wх В(х) ≠ U и А∩В≠ Ø. Их содержание отвечает условию ù"х(А(х) V B(х)). На 15-й схеме дано универсальное и исчерпывающее пересечение. Оба понятия здесь также являются совместимыми. На схеме этот вид пересечения изображен частичным наложением площади А на площадь В (либо наоборот, если это является принципиально важным). В данном случае имеет место универсальное пересечение, такое, когда оба понятия, мыслимые вместе, исчерпывают весь объем универсума. Например, понятия «человек, старше двадцати лет» и «человек моложе тридцати лет» на универсуме людей находятся в таком отношении.
6) Отношение противоречия отображено в трех модельных схемах. 14-ю схему можно трактовать, как дополнение одного понятия другим. Здесь нет отношения включения. Такие противоречащие понятия несовместимы и оба вместе исчерпывают весь объем универсума. На 2-й и 3-й схемах представлены два вида универсального противоречия, при котором имеет место отношение включения. Понятие хА(х) находится в отношении противоречия с понятием хВ(х):
Wх ùА(х)= Wх В(х) – для 2-ой схемы
Wх А(х)= Wх ùВ(х) - для 3-й схемы
7) Отношения соподчинения. Данное отношение задано следующими условиями: понятия хА(х) и хВ(х) не находятся в отношении включения, не являются пересекающимися, они несовместимы и не исчерпывают всего универсума. Данный вид отношений представлен единственной модельной схемой –13-ой.
Из перечня модельных схем исключена 16-я схема, отображающая противоположные понятия.


 Затруднения, возникающие при анализе отношений между этими понятиями, были уже предметом нашего обсуждения. Снять эти затруднения удается, если понимать противоположные понятия, как соподчиненные, а они именно таковы. При таком подходе они полностью укладываются по своим объемным характеристикам в 13-ю схему.
Затруднения, возникающие при анализе отношений между этими понятиями, были уже предметом нашего обсуждения. Снять эти затруднения удается, если понимать противоположные понятия, как соподчиненные, а они именно таковы. При таком подходе они полностью укладываются по своим объемным характеристикам в 13-ю схему.
Пятнадцать модельных схем не отражают всей полноты отношений между понятиями. Если понятия являются сложными и их объемы одновременно находятся в различных отношениях, то выявить богатство отношений между ними требуют иного подхода. Различные части объемов сложных понятий могут находиться в самых разнообразных отношениях друг с другом и в этом смысле требуют построения не одной, а многих схем для выявления этих отношений. Более предпочтительным для таких понятий является способ построения диаграмм, знание о котором требует предварительного знакомства с алгеброй Буля.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 827; Нарушение авторских прав?; Мы поможем в написании вашей работы!