Передаточное отношение для тел совершающих вращательное движение

Рассмотрим два тела 1 и 2, совершающих вращательное движение соответственно вокруг центров 0₁ и 0₂ с угловыми скоростями w ₁ и w ₂ (рис. 11.6). Причем нам неизвестно связаны эти тела между собой или нет. Как отмечено выше, полюс относительного вращения этих тел будет лежать в такой общей точке этих тел, где вектора скоростей как первого, так и второго тела будут равны. Для скоростей любой точки первого тела V_A = w₁×l_A01 , для любой точки второго - V_В = w ₂×l_В02 . Равенство векторов скоростей по направлению для тел, совершающих вращательное движение, возможно только на линии соединяющей центры вращения тел. Поэтому полюс относительного вращения должен лежать на этой линии. Для определения положения полюса на линии центров составим следующее уравнение

Рис 11.6

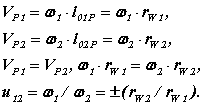
Таким образом, полюс относительного вращения звеньев лежит на линии центров и делит ее на отрезки обратно пропорциональные угловым скоростям.

Теорема Виллиса. Передаточное отношение между звеньями совершающими вращательное движение прямопропорционально отношению угловых скоростей и обратно пропорционально отношению расстояний от центров вращения до полюса.

Знак перед отношением показывает внешним (знак +, зацепление внутреннее) или внутренним (знак -, зацепление внешнее) образом делит полюс линию центров на отрезки r_w1 = l _01P и r_w2 = l _02P. Данная формула получена из рассмотрения вращательного движения двух тел, при этом тела могут быть и не связаны между собой.

Воспользуемся методом обращенного движения и рассмотрим движение нашей системы относительно звена 1. Для этого к скоростям всех звеньев механизма добавим - w ₁. Тогда скорости звеньев изменятся следующим образом:

Движение механизма:	Звено 1	Звено 2	Звено 0
исходное	w 1	w 2	w 0 = 0
относительно звена 1	w 1 - w1 = 0	w 21 = w2 - w 1	w 1 = - w01

Скорость любой точки звена 2 в относительном движении будет равно его угловой скорости в этом движении умноженной на расстояние от этой точки до полюса относительного вращения, т. е.

Перейдем к рассмотрению двух тел 1 и 2, совершающих вращательное движение, соответственно вокруг центров 0₁ и 0₂ с угловыми скоростями w ₁ и w₂, и образующих между собой высшую кинематическую пару К (рис. 11.7).

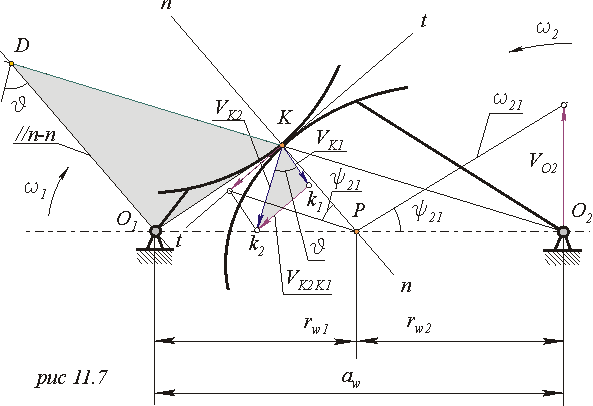
Условием существования высшей кинематической пары является условие неразрывности контакта звеньев, которое заключается в том, что проекции скоростей звеньев в точке контакта на контактную нормаль к профилям должны быть равны

т.е. скалярное произведение вектора относительной скорости в точке контакта на орт нормали равно нулю. Это условие обеспечивается, если скорость относительного движения контактных точек лежит на касательной (в пространстве в касательной плоскости). При выполнении этого условия профили не отстают друг от друга (нарушение контакта приведет к исчезновению пары), и не внедряются друг в друга

(что при принятом допущении о абсолютно жестких звеньях, невозможно).

Как было показано выше скорость относительного скольжения в точке контакта равна

где l_KP - расстояние от контактной точки до полюса относительного вращения. Так как V_K2K1 перпендикулярна l_KP >, а V_K2K1 должна лежать на касательной, то l_KP является нормалью к профилям в точке контакта. То есть контактная нормаль к профилям в высшей паре пересекает линию центров в полюсе относительного вращения.

Основная теорема зацепления.

Формулировка анализа. Контактная нормаль к профилям высшей пары пересекает линию центров в полюсе относительного вращения звеньев (то что полюс делит линию центров на отрезки обратно пропроциональные угловым скоростям было доказано выше).

Формулировка синтеза. Профили в высшей кинематической паре должны быть выполнены так, чтобы контактная нормаль к ним проходила через полюс относительного вращения звеньев.

Так как положение полюса на линии центров определяет передаточное отношение механизма, то профили удовлетворяющие основной теореме зацепления обеспечивают заданный закон изменения передаточного отношения или являются сопряженными.

Скорость скольжения в высшей КП или перовое следствие основной теоремы зацепления.

Скорость скольжения профилей в высшей КП равна произведению скорости относительного вращения на расстояние от контактной точки до полюса зацепления.

где верхний знак относится к внешнему зацеплению, нижний - к внутреннему. Зацепление считается внешним, если полюс делит линию центров внутренним образом и направления угловых скоростей звеньев противоположны, и внутренним, если полюс делит линию центров внешним образом (Рис. 17.8) и направления угловых скоростей одинаковы.

Из формулы видно, что скорость скольжения во внутреннем зацеплении много меньше, чем во внешнем.

Определение центра вращения ведущего звена или второе следствие основной теоремы зацепления.

Из схемы, изображенной на рис. 11.7, видно, что

т.е. отрезок l_KD, отсекаемый от луча, проведенного из точки О₂ через точку K, прямой параллельной контактной нормали, равен передаточной функции точки K₂.

Второе следствие основной теоремы зацепления.

Формулировка синтеза. Если на продолжении луча, проведенного из точки О₂ через точку K, отложить от точки K отрезок длиной l_KD = V_K2 / w₁ = V_qK2 и через конец этого отрезка провести прямую параллельную контактной нормали, то эта прямая пройдет через центр вращения ведущего звена точку О₁.

С использованием этого свойства механизма с высшей парой при проектировании кулачковых механизмов определяют радиус начальной шайбы по допустимому углу давления.

Формулировка анализа. Луч проведенный через центр вращения ведущего звена точку О₂ параллельно контактной нормали, отсекает на луче проведенном из точки О₂ через точку K отрезок l_KD = V_K2 / w₁ = V_qK2 , равный передаточной функции точки K₂.

Лекция 11

Плоские кулачковые механизмы

Большое распространение в машиностроении имеют так называемые кулачковые механизмы. Простейший кулачковый механизм состоит из ведущего звена, элемент которого имеет переменную кривизну,— кулачка 1, совершающего вращательное движение, и ведомого звена — толкателя 2, совершающего возвратно-поступательное движение (рис. 1).

Рис.1

Кулачок и толкатель образуют высшую кинематическую пару 2-го класса. Как известно, низших кинематических пар 1-го класса в плоских механизмах всего два вида — вращательная и поступательная, а высших кинематических пар — бесчисленное множество. Поэтому при помощи кулачковых механизмов, в состав которых входят высшие кинематические пары, можно легко и просто осуществить почти любой наперед заданный закон движения ведомого звена, для чего требуется лишь подобрать соответствующий профиль кулачка.

В практике часто необходимо иметь движение ведомого звена с остановками при непрерывном движении ведущего звена, что очень легко достигается при помощи кулачковых механизмов. Для этого следует в соответствующем месте сделать профиль кулачка по дуге окружности с центром на оси вращения кулачка.

Простота конструкции и возможность осуществления почти любого заданного закона движения ведомого звена является основными достоинствами кулачковых механизмов.

Кулачковые механизмы имеют очень широкое применение в станках-автоматах.

По видам движения кулачка и толкателя кулачковые механизмы делятся в основном на следующие типы:

а) механизмы, в которых вращательное движение кулачка преобразуется в возвратно-поступательное движение толкателя (рис. 1, рис. 2, а);

Рис.2

б) механизмы, в которых вращательное движение кулачка преобразуется в возвратно-вращательное движение толкателя (рис.2, б);

Рис. 2

механизмы, в которых возвратно-поступательное движение кулачка преобразуется в возвратно-поступательное движение толкателя (рис. 2, в);

Рис. 2

г) механизмы, в которых возвратно-поступательное движение кулачка преобразуется в возвратно-вращательное движение толкателя (рис. 2, г).

Рис. 2

Наиболее часто на практике применяются кулачковые механизмы первых двух типов. Кулачковые механизмы первого типа могут быть центральными, когда линия движения толкателя проходит через ось вращения кулачка (см. рис.2, а), и нецентральными, или смещенными, когда линия движения толкателя не проходит через ось вращения кулачка, а смещена от нее на некоторую величину е, называемую эксцентриситетом (см. рис. 1).

Толкатели кулачковых механизмов в зависимости от элементов, которыми они касаются кулачка, делятся на следующие виды.

1. Остроконечный толкатель (рис. 3, а, г), конец которого выполнен очень малым радиусом. Недостатком таких толкателей является их низкая износостойкость, вследствие чего они могут применяться только в тихоходных кулачковых механизмах при незначительных передаваемых усилиях.

Рис. 3

2. Сферический грибовидный толкатель (рис. 3, б), профиль которого очерчен по сфере.

Рис. 3

3. Плоский (тарельчатый) толкатель (рис. 3, в, д), профилем которого является плоскость. Достоинство такого толкателя — благоприятное направление усилий. Однако при плоском толкателе кулачок должен быть выпуклым по всему профилю.

Рис. 3

Толкатель, снабженный цилиндрическим роликом (см. рис. 2). Достоинством кулачкового механизма с таким толкателем по сравнению со всеми предыдущими является его износостойкость, так как здесь трение скольжения профилей высшей кинематической пары заменяется трением качения. Однако при толкателе с роликом, естественно, увеличиваются размеры кулачкового механизма.

Рис. 4

Во время работы кулачкового механизма возникают инерционные усилия, направленные на отрыв рабочей поверхности толкателя от профиля кулачка. Поэтому одним из важнейших требований к кулачковым механизмам является то, что кулачок и толкатель должны быть постоянно в соприкосновения, т. е они должны быть замкнуты.

Замыкание высшей кинематической пары кулачок — толкатель применяется либо кинематическое (геометрическое), либо силовое.

Примером кинематического замыкания может служить кулачковый механизм с пазовым кулачком, схема которого изображена на рис. 4. В паз кулачка, очерченный двумя эквидистантными (равноотстоящими) поверхностями, входит ролик толкателя, произвольное перемещение которого таким образом исключается.

Силовое замыкание в большинстве случаев (рис. 5) осуществляется при помощи пружины. Реже
для создания замыкающей силы применяются пневматические или гидравлические устройства.

Рис. 5

Иногда для медленно движущихся кулачковых механизмов силовое замыкание осуществляется при помощи грузов. Однако при таком замыкании сильно возрастают габариты механизма, и оно применяется очень редко.

Необходимость замыкания кулачковых механизмов является их недостатком, так как это усложняет конструкцию. Другим недостатком кулачковых механизмов является сложность изготовления профиля кулачка, особенно когда от него требуется высокая точность.

Кроме рассмотренных плоских кулачковых механизмов, в технике применяются пространственные кулачковые механизмы. Схемы некоторых видов этих механизмов представлены на рис. 6, а, б.

Рис. 6

При изучении кулачковых механизмов возникают две задачи: исследование существующих (заданных) кулачковых механизмов (анализ) и проектирование новых кулачковых механизмов по заданным условиям (синтез).

Дата добавления: 2014-01-04