Центральный кулачковый механизм с острым толкателем

Определение положений кулачковых механизмов

Задачи анализа кулачковых механизмов сводятся к определению положений толкателя в зависимости от положения кулачка и установлению скоростей и ускорений толкателя.

Определение положений начнем с наиболее простого центрального кулачкового механизма с острым толкателем.

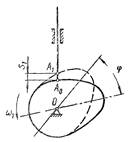Пусть дан кулачковый механизм (рис. 7). Требуется определить положение толкателя при повороте кулачка на заданный угол φ.

Рис.7

Определение положения толкателя в зависимости от положения кулачка можно было бы произвести обычным способом, т. е. повернуть кулачок на заданный угол φ (пунктирная линия) и найти точку пересечения линии движения толкателя с профилем кулачка (точка А₁), которая представляет искомое положение конца толкателя. Величина 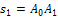есть перемещение толкателя при повороте кулачка на заданный угол φ.

Однако такое построение сложно и неточно, так как требует дополнительного построения сложного профиля кулачка. Особенно сложно построение таким способом, если исследование следует произвести за весь цикл движения, т. е. за полный оборот кулачка. В этом случае пришлось бы строить целый ряд профилей кулачка.

Задача значительно облегчается, если применить так называемый метод обращения движени я. Этот метод заключается в следующем.

Сообщим всему кулачковому механизму вместе со стойкой вращательное движение вокруг оси вращения кулачка О с угловой скоростью ω₁ (рис. 8).

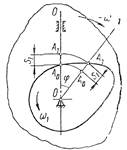
Рис. 8

Относительное движение звеньев от этого не изменится. Но тогда кулачок относительно неподвижных осей координат станет неподвижным, а толкатель вместе со стойкой будет вращаться вокруг оси вращения кулачка в противоположную сторону с угловой скоростью, равной по абсолютной величине угловой скорости кулачка. Поэтому вместо того, чтобы поворачивать кулачок на заданный угол φ, следует повернуть толкатель (вместе со стойкой) на этот же угол, но в противоположное направление. Линия движения толкателя при этом займет положение 0—1, которое является искомым относительным положением толкателя. Точка пересечения линии 0—1 с профилем кулачка А′₁ есть искомое относительное положение конца толкателя.

Для определения действительного искомого положения конца толкателя достаточно радиусом ОА′₁ сделать засечку на действительной линии движения толкателя. Полученная точка А₁ есть действительное искомое положение конца толкателя. Отрезок 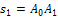есть искомое перемещение толкателя. Это перемещение можно измерить и по линии относительного положения толкателя 0—1, для чего надо на этой линии сделать засечку радиусом ОА₀ (точка А'₀). Отрезок А'₀А′₁ также есть искомое перемещение толкателя .

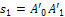При указанных построениях положение стойки показывать не следует. Необходимо наносить лишь относительное положение линии движения толкателя.

Дата добавления: 2014-01-04