
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция №20
|
|
|
|
Давление в жидкостях и газах. Распределение давления в жидкостях и газах, находящихся в состоянии равновесия. Закон Паскаля. Сила Архимеда. Условие плавания тел. Стационарное слоистое движение жидкости. Уравнение неразрывности струи. Уравнение Бернулли для идеальной жидкости и его применение. Формула Торичелли. Реакция вытекающей струи.
Лекция № 19
Жидкости и газы рассматривают в механике как сплошные среды, непрерывно заполняющие часть пространства. Так же как и твердые тела, жидкости и газы принимают за систему материальных точек, каждая из которых является элементарным объемом.
Представление жидкости или газа в виде системы неизменно связанных между собой элементов допустимо, если жидкость покоится или движется как целое. В этом случае мы можем часть объема жидкости (или весь объем) рассматривать как твердое тело и применять к нему законы механики твердого тела. Этот прием носит название принципа отвердения.
Выделим внутри жидкости произвольный элемент и рассмотрим действующие на него силы. Их можно разделить на внутренние (действующие между частицами элемента) и внешние (действующие со стороны соседних элементов). Внутренние силы взаимно уравновешиваются, потому мы вправе их действия не учитывать.
Внешние силы, как и в случае твердого тела, разделим на массовые (действующие на каждую материальную частицу элемента) и поверхностные (приложенные к поверхности элемента). Вообще говоря, было бы важно знать и внутренние силы, чтобы характеризовать напряженное состояние внутри выделенного элемента жидкости. Однако в гидромеханике ограничиваются указанием некоторого среднего напряженного состояния для объема в целом. В самом деле, если в выбранном элементе находится большое число молекул, движущихся хаотически, то установить детальную картину распределения взаимодействия между ними практически невозможно.
На первый взгляд определение среднего напряженного состояния внутри выделенного элемента тоже невозможно, так как внутренние силы при суммировании уравнений, составленных для отдельных элементов, взаимно уничтожаются. Однако это затруднение можно обойти, если с помощью какого-либо приема внутренние силы сделать внешними.
Как и для сплошного твердого тела, результирующую внутренних сил, отнесенную к единице площади сечения, называют напряжением.
В покоящейся жидкости напряжения могут быть направлены только нормально к поверхности элемента. Это свойство обусловлено легкоподвижностью частиц жидкости. Если возникнет хотя бы малая составляющая внутренних сил в направлении, касательном к поверхности элемента, частицы жидкости придут в движение.
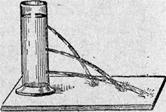
Возникновение внутренних напряжений в жидкости легко установить на опыте. Поместим жидкость в замкнутый сосуд с поршнем (рис.1).
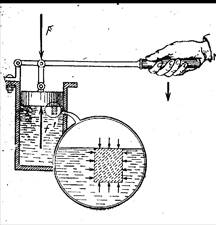
рис № 1 Возникновение внутренних напряжений в жидкости.
Положим, на поршень действует сила F. Если при этом некоторый слой жидкости, непосредственно прилегающий к поршню, находится в равновесии, то, следовательно, на него со стороны соседних слоев жидкости действует сила, результирующая которой уравновешивает силу, действующую со стороны поршня.
В большинстве случаев силы, действующие на поверхность элемента жидкости, сжимают его, т. е. направлены внутрь элемента. Силы, направленные по нормали к поверхности объема внутрь его, называются силами давления.
Давление имеет размерность силы, деленной на площадь. За единицу давления принимают в СИ Н/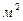
Давление на малой площадке, определяющей точку в покоящейся жидкости, одинаково при любой ориентации площадки.
Выделим внутри жидкости произвольную трехгранную призму (рис.2)
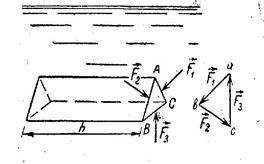
рис. № 2.Давление в плоскости жидкости не зависит от ориентации площадки.
Силы давления, действующие на противоположные основания призмы, равны по величине и противоположны по направлению.
Силы давления Ft, F2, F3 на боковые грани призмы перпендикулярны к ним.
Построим на этих силах силовой треугольник abc (рис №2). Его стороны перпендикулярны сторонам треугольника ABC, полученного сечением призмы плоскостью, параллельной основанию и проходящей через векторы 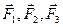 . Следовательно, треугольники ABC и abc подобны:
. Следовательно, треугольники ABC и abc подобны:
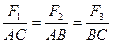 . (1)
. (1)
Напряжение на гранях призмы получим, если разделим силы 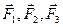 на площади соответствующих граней. Но площади граней равны AC*h, AB*h, BC*h, где h— высота призмы. Следовательно,
на площади соответствующих граней. Но площади граней равны AC*h, AB*h, BC*h, где h— высота призмы. Следовательно,
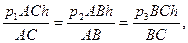 (2)
(2)
или 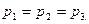
Таким образом, давление в покоящейся жидкости (статическое давление) одно и то же на всех трех гранях. Так как призма была выбрана произвольно, то условие (2) будет выполняться для любой призмы (любой величины и любым образом ориентированной).
Уменьшая размеры призмы, мы придем к малым площадкам, различно ориентированным около некоторой точки. Как следствие этого положения может быть получен закон Паскаля: давление в любой точке покоящейся жидкости одинаково по всем направлениям и одинаково передается во все стороны.
Закон Паскаля используется в так называемых гидравлических прессах. Схема такого пресса изображена на рис. 3.
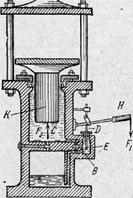
рис.№ 3 Схема гидравлическрго пресса
.Он состоит из двух сообщающихся между собой цилиндрических полостей С и Е, закрытых поршнями К и D, которые могут перемещаться вверх и вниз. Когда на поршень D действует сила 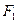 , приложенная к рычагу H, то создаваемое ею давление передается жидкостью из цилиндра Е через вентиль В в цилиндр С. Сила
, приложенная к рычагу H, то создаваемое ею давление передается жидкостью из цилиндра Е через вентиль В в цилиндр С. Сила 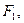 действующая на поршень D, относится к силе F2, действующей со стороны жидкости на поршень К, как площадь сечения поршня D к площади сечения поршня К. При большой разнице размеров поршней (площади их сечений) можно получить большой выигрыш в силе, который и используется в гидравлическом прессе. Гидравлические прессы широко применяются в технике (при штамповке изделий, при подъеме тяжестей, например гидравлические подъемники автомобилей.
действующая на поршень D, относится к силе F2, действующей со стороны жидкости на поршень К, как площадь сечения поршня D к площади сечения поршня К. При большой разнице размеров поршней (площади их сечений) можно получить большой выигрыш в силе, который и используется в гидравлическом прессе. Гидравлические прессы широко применяются в технике (при штамповке изделий, при подъеме тяжестей, например гидравлические подъемники автомобилей.
Выделим в однородной покоящейся жидкости элемент (рис. 4) в виде прямоугольного параллелепипеда с площадью основания  S и гранями, параллельными направлению силы тяжести и имеющими высоту
S и гранями, параллельными направлению силы тяжести и имеющими высоту 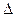 z
z
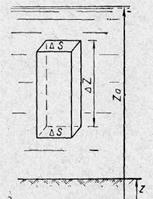
. Рис.№4 К выводу распределения гидростатического давления.
Так как жидкость, а вместе с ней и выделенный элемент покоятся, то, следовательно, давления на его боковые грани уравновешиваются. Для того чтобы найти условие равновесия параллелепипеда в вертикальном направлении, надо учесть давления 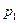 и
и 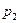 , действующие на нижнее и верхнее основания, и силу тяжести, действующую на параллелепипед. К верхнему основанию приложена сила
, действующие на нижнее и верхнее основания, и силу тяжести, действующую на параллелепипед. К верхнему основанию приложена сила 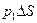 , направленная вниз. Сила тяжести, действующая на весь параллелепипед, равна
, направленная вниз. Сила тяжести, действующая на весь параллелепипед, равна 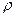
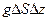 , где
, где 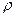 — плотность жидкости, g —ускорение силы тяжести. На нижнее основание действует сила
— плотность жидкости, g —ускорение силы тяжести. На нижнее основание действует сила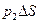 , направленная вверх. Применив принцип отвердения для равновесия выделенного элемента жидкости в вертикальном направлении, напишем условие, аналогичное условию равновесия твердого тела:
, направленная вверх. Применив принцип отвердения для равновесия выделенного элемента жидкости в вертикальном направлении, напишем условие, аналогичное условию равновесия твердого тела:
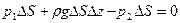 (3)
(3)
или
| (12.4)( |
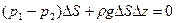 (4)
(4)
Уменьшая параллелепипед и полагая высоту и площадь его основания в пределе бесконечно малыми, получим из формулы (4):
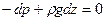 (5)
(5)
(для равновесия элементарного параллелепипеда dp должно быть направлено противоположно силе тяжести, что и показывает знак «минус»).
Чтобы найти закон распределения давления в жидкости по высоте конечной величины, проинтегрируем правую и левую части этого уравнения:
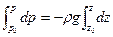 (6)
(6)
где р0 — давление на высоте z0 над условной горизонтальной плоскостью, р — давление в данной точке, находящейся на высоте z. Получим:
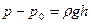 , (7)
, (7)
где 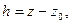
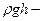 давление на нижнее основание призмы, создаваемое весом столба жидкости высотой h. Введя объёмный вес
давление на нижнее основание призмы, создаваемое весом столба жидкости высотой h. Введя объёмный вес 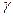 , перепишем уравнение (7) в виде:
, перепишем уравнение (7) в виде:
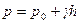 . (8)
. (8)
Это уравнение называется гидростатическим уравнением.
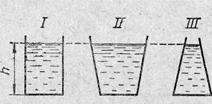
Давление жидкости на дно не зависит от формы сосуда, а только от высоты ее поверхности над дном (рис. 5). Давление на элемент боковой стенки сосуда зависит от его глубины под поверхностью жидкости (рис.6).
|
рис.№5 Гидростатический парадокс:
давление жидкости на дно зависит не
от формы сосуда, а только о высоты её
поверхности над дном.
|
рис.№6 Давление на элемент боковой поверхности сосуда.
Свободная поверхность однородной жидкости в сообщающихся сосудах устанавливается на одной высоте (рис. 7). В случае неоднородных жидкостей высоты их свободных поверхностей в сообщающихся сосудах над нулевой плоскостью обратно пропорциональны плотностям жидкостей (рис. 8).

|
|
рис.№7 Сообщающиеся сосуды.
Рис. № 8Вода и ртуть в сообщающихся сосудах.
Архимед установил, что кажущийся вес тела, погружённого в жидкость, меньше действительного на столько, сколько весит вытесненная телом жидкость.
Выделим мысленно объём жидкости такой же поверхности, как и поверхность данного твёрдого тела. Вообразим, что выделенная нами жидкость затвердела, сохраняя неизменной свою плотность. Равновесие в жидкости при этом, очевидно, не нарушиться. Следовательно, вес отвердевшей части жидкости равен силе давления, с которой на него действует окружающая жидкость. Другими словами, результирующая давлений покоящейся жидкости на произвольную замкнутую поверхность равна по величине и противоположна по направлению весу жидкости, заключённой внутри этой поверхности.
Следовательно, если мы поместим в жидкость твёрдое тело, которое займёт тот же объём, что и отвердевшая часть жидкости, то на него будет действовать выталкивающая сила, равная весу вытесненной им жидкости,
Закон Архимеда используется при оценке плавучести и остойчивости кораблей.
Условием плавания тел в жидкости, очевидно, является равенство его веса весу вытесненной им жидкости.
Представим себе в жидкости трубку, боковая поверхность которой составлена из прилегающих друг к другу линий тока (рис. 9).

|
рис. № 9. Трубка тока.
Если течение стационарно, то все частицы жидкости, заключенные внутри этой поверхности, останутся внутри нее во все время движения. Таким образом, поверхность, образованная линиями тока в жидкости, представляет собой как бы непроницаемую трубку. Часть жидкости, ограниченная линиями тока, пронизывающими замкнутый контур, называется трубкой тока. Размеры и положения контура выбираются такими, чтобы в его пределах скорость течения можно было считать постоянной и направленной по нормали к контуру.
Очевидно, всякое движение жидкости, происходящее без разрывов сплошности (без пузырьков и «пустот»), должно удовлетворять закону сохранения массы. Масса 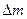 жидкости, прошедшей за время
жидкости, прошедшей за время 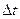 через какое-либо поперечное сечение трубки тока S, равна:
через какое-либо поперечное сечение трубки тока S, равна:
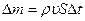
где 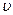 — скорость частиц, постоянная в данном сечении,
— скорость частиц, постоянная в данном сечении, 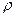 — плотность жидкости в том же сечении.
— плотность жидкости в том же сечении.
При стационарном потоке за один и тот же интервал времени 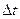 через два разных сечения трубки тока
через два разных сечения трубки тока 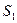 и S2 должны проходить одинаковые массы жидкости. В противном случае масса жидкости, заключенной в объеме трубки между выбранными сечениями, изменялась бы, и течение перестало быть стационарным. Поэтому для стационарного течения
и S2 должны проходить одинаковые массы жидкости. В противном случае масса жидкости, заключенной в объеме трубки между выбранными сечениями, изменялась бы, и течение перестало быть стационарным. Поэтому для стационарного течения
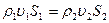 (9)
(9)
Для капельных жидкостей и для газов, когда сжимаемость последних роли не играет, можно считать плотность постоянной. Тогда уравнение (9) запишется в виде
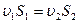 ,
,
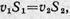
|
или
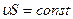 (10)
(10)
Произведение величины скорости течения несжимаемой жидкости на величину поперечного сечения трубки тока есть величина постоянная для данной трубки тока
(теорема неразрывности).
Рассмотрим участок трубки тока, ограниченный двумя поперечными сечениями А В и CD, площади которых соответственно равны St и S2 (рис. 10). Площади сечений возьмем достаточно малыми, чтобы скорости частиц и давления в пределах каждого из сечений можно было считать постоянными.
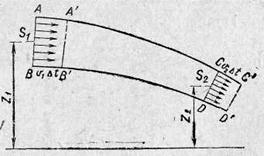
|
Рис.№10. К выводу теоремы Бернулли.
Перемещаясь от сечения АВ к сечению CD, жидкость переходит в суженную часть трубки и, как следует из уравнения неразрывности, движется ускоренно. Значит, на жидкость, находящуюся в данный момент в суженной части трубки, действует со стороны жидкости, находящейся в более широкой ее части, некоторая сила, которая может возникнуть только вследствие разности давлений в различных сечениях трубки. Сила направлена в сторону узкой части трубки, следовательно, в местах сужений давление меньше, чем в местах расширений.
Установим связь между давлением и скоростью жидкости в разных сечениях трубки, ограничиваясь рассмотрением идеальной жидкости (не учитывая вязкость и сжимаемость жидкости), что позволит нам считать работу внутренних сил в жидкости равной нулю. Трение между жидкостью и стенками сосуда будем считать отсутствующим (это позволит нам выбрать трубку в произвольном месте потока); движение — вполне установившимся (стационарным, при этом масса и энергия идеальной жидкости, заполняющей некоторый объем трубки тока, остаются постоянными во все время движения); линии тока — слабо искривленными (что позволит пренебречь центростремительным ускорением частиц жидкости и связанным с ним изменением давления в поперечном сечении трубки тока).
К жидкости, заключенной в рассматриваемом объеме, можно применить второй закон динамики и написать для нее уравнение движения. Но так как в идеальной жидкости нет рассеяния механической энергии, то результат проще получить, применяя закон сохранения энергии.
Покоящаяся жидкость массой т обладает потенциальной энергией:
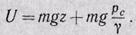 (11)
(11)
Если жидкость движется со скоростью о, то она обладает еще кинетической энергией, и полное значение энергии будет:
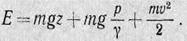 (12) (12)
|
В выражении (12) давление р отлично от давления рс, входящего в формулу (11), так как жидкость могла приобрести кинетическую энергию только за счет преобразования потенциальной энергии. При соблюдении первых трех из перечисленных выше ограничений энергия жидкости, заключенной в выделенном объеме, остается неизменной. Следовательно, энергия  жидкости массой
жидкости массой 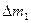 , втекающей в объем за время
, втекающей в объем за время 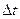 через сечение
через сечение 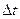 , должна быть равна энергии
, должна быть равна энергии 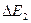 жидкости массой
жидкости массой 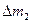 , вытекающей за то же время через сечение
, вытекающей за то же время через сечение 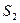 . Если плотность жидкости
. Если плотность жидкости 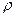 , то
, то

Приравнивая правые части этих равенств и деля их на
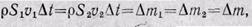 (13)
(13)
получим:
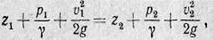 (14)
(14)
или, учитывая, что 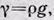
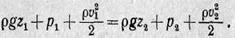 (15)
(15)
Так как сечения S1 и S2 взяты произвольно, то вообще для любого сечения данной трубки тока
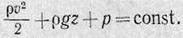 (16)
(16)
Это уравнение, полученное Д. Бернулли (1738 г.), связывает изменение давления в стационарном потоке идеальной жидкости с изменением скорости течения и геометрической высоты.
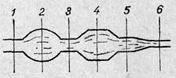
|
рис. № 11. Уравнение Бернулли можно применять к сечениям 1,2,3,4,5,6.
Закон Бернулли представляет собой закон постоянства полной удельной энергии частиц движущейся идеальной жидкости при стационарном течении. Формулы (16) и (15) выражают тот же закон сохранения энергии для единицы объема жидкости: 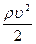 —кинетическая энергия единицы объема жидкости,
—кинетическая энергия единицы объема жидкости, 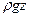 — его потенциальная энергия в поле силы тяжести, p — работа силы давления при подъеме единицы объема на единицу высоты.
— его потенциальная энергия в поле силы тяжести, p — работа силы давления при подъеме единицы объема на единицу высоты.
В выражении (14) все члены имеют размерность длины: 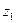 и— геометрические высоты,
и— геометрические высоты, 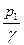 и— пьезометрические высоты и — скоростной, или динамический, напор.
и— пьезометрические высоты и — скоростной, или динамический, напор.
Таким образом, в теореме Бернулли отражены два физических факта: 1) сумма потенциальной энергии и кинетической энергии на всем протяжении данной трубки тока — величина постоянная; 2) сумма трех высот: пьезометрической, геометрической и скоростной — остается постоянной в каждом сечении трубки.
Рассмотрим несколько практически важных применений теоремы Бернулли.
а) Скорость истечения из отверстия. Рассмотрим задачу, решенную еще Д. Бернулли, об истечении жидкости из открытого сосуда через малое отверстие под действием силы тяжести. Пусть имеется широкий сосуд с жидкостью (рис. 171), уровень которой стоит на высоте z1 над дном сосуда. На высоте 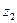 имеется малое (по сравнению с сечением сосуда) отверстие с плавно закругленными краями. На свободную поверхность жидкости в сосуде действует атмосферное давление р1 такое же давление действует и на поверхность вытекающей струи (сосуд невысок). Так как площадь сечения сосуда велика по сравнению с площадью сечения отверстия, то скорость движения частиц свободной поверхности
имеется малое (по сравнению с сечением сосуда) отверстие с плавно закругленными краями. На свободную поверхность жидкости в сосуде действует атмосферное давление р1 такое же давление действует и на поверхность вытекающей струи (сосуд невысок). Так как площадь сечения сосуда велика по сравнению с площадью сечения отверстия, то скорость движения частиц свободной поверхности 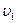 мала по сравнению со скоростью частиц в отверстии
мала по сравнению со скоростью частиц в отверстии 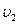 и ею можно пренебречь.
и ею можно пренебречь.
Линии тока в отверстии можно считать параллельными и направленными перпендикулярно плоскости его сечения. Все линии тока начинаются на поверхности жидкости, которая медленно снижается по мере вытекания жидкости из сосуда. Тогда для каждого момента времени мы можем написать уравнение Бернулли:

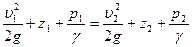 ,
,
где величины с индексом 1 относятся к сечению, совпадающему со свободной поверхностью жидкости в сосуде, а с индексом 2 — к сечению струи в отверстии. Но по условию
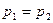 и
и 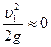 .
.
Тогда
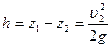 ,
,
откуда
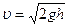 ,
,
т. е. скорость частиц в отверстии такова, как если бы частицы под действием собственного веса падали с высоты h. Формула эта носит название формулы Торричелли.
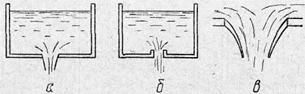
рис.№12. Сжатие струи:
а)отверстие без насадки, б)цилиндрическая насадка. в)насадка по форме струи
Решая задачу с помощью теоремы Бернулли, мы пренебрегали вязкостью жидкости и считали линии тока перпендикулярными плоскости сечения отверстия. На самом же деле частицы подходят к отверстию по криволинейным траекториям и не могут в отверстии внезапно изменить направление движения, вследствие чего струя оказывается несколько сжатой и площадь ее сечения меньше площади отверстия (рис. 12).
Для проверки формулы Торричелли проще всего измерить объем жидкости, вытекающей из отверстия за время 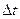 , и, разделив его на время, получить величину расхода жидкости Q, которая должна удовлетворять равенству:
, и, разделив его на время, получить величину расхода жидкости Q, которая должна удовлетворять равенству:
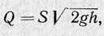
где S — площадь сечения отверстия.
При сравнении фактического и вычисленного расхода жидкости первый оказывается меньше второго. Коэффициент пропорциональности между ними 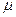 называют в гидравлике коэффициентом истечения или коэффициентом расхода:
называют в гидравлике коэффициентом истечения или коэффициентом расхода:
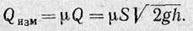
Коэффициент 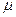 различен для разных жидкостей (зависит от их вязкости) и отверстий разной формы (зависит от степени сжатия струи).
различен для разных жидкостей (зависит от их вязкости) и отверстий разной формы (зависит от степени сжатия струи).
б) Некоторые приборы для измерения давлений и скоростей в жидкости
(трубки Пито-Прандтля, трубка Орлова).
в) Использование в технике зависимости давления в жидкости от величины её скорости.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 567; Нарушение авторских прав?; Мы поможем в написании вашей работы!