Вынужденные колебания. Они возникают при действии на систему внешней периодически изменяющейся силы (вынуждающей силы) , (22)

Они возникают при действии на систему внешней периодически изменяющейся силы (вынуждающей силы) 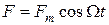, (22)

где 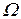- круговая частота вынуждающей силы.

Дифференциальное уравнение вынужденных колебаний с учетом затухания запишется в виде:

m(d²x/dt²) = -kx - r(dx/dt) + F_mcos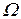t.

Перепишем это уравнение в виде:

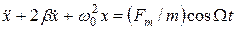. (23)

Таким образом, получили линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Решением такого уравнения будет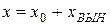, где 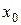– общее решение однородного уравнения (23), (т. е. уравнения (23) с правой частью, равной нулю). Согласно (17)

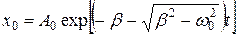
и с течением времени 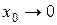. Поэтому .

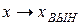Из решения (23) следует, что 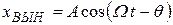(24)

где 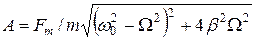, (25)

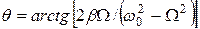. (26)

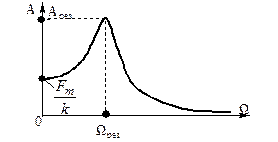Из анализа (25) следует, что хотя амплитуда вынуждающей силы F_m, остается постоянной, амплитуда А вынужденных колебаний зависит от частоты 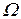вынуждающей силы.

Рис. 11

Исследуя (25) на экстремум, можно показать, что только при резонансной частоте

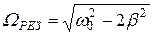(27)

амплитуда вынужденных колебаний достигает максимальной величины:. (28)

Это явление называется резонансом.

На рис. 11 приведена зависимость амплитуды А вынужденных колебаний от частоты 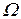вынуждающей силы, которая определяется формулой (25); (откуда: при 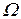= 0 находим 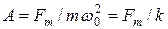, а при 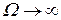имеем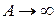, что объясняется инерционностью колебательной системы).

Явление резонанса, состоящее в резком увеличении амплитуды колебаний при приближении частоты вынуждающей силы к резонансной частоте, широко используется в технике. Его следует учитывать при конструировании машин, кораблей, самолетов и т.д. Необходимо, чтобы их резонансные частоты не совпадали с частотой вынуждающих внешних воздействий.

8.Автоколебания

При затухающих колебаниях энергия системы расхо­дуется на преодоление сопротивления среды. Если вос­полнять эту убыль энергии, колебания станут незатуха­ющими. Пополнение энергии системы может осуществ­ляться за счет толчков извне, однако эти толчки должны сообщаться системе в такт с ее колебаниями, в против­ном случае они могут ослабить колебания и даже прекра­тить их совсем. Можно сделать так, чтобы колеблющаяся система сама управляла внешним воздействием, обеспе­чивая согласованность сообщаемых ей толчков со своим движением. Такая система называется автоколеба­тельной, а совершаемые ею незатухающие колеба­ния— автоколебаниями.

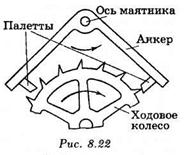
В качестве примера автоколебательной системы рас­смотрим часовой механизм. Маятник часов насажен на одну ось с изогнутым рычагом — анкером (рис.). На концах анкера имеются выступы специальной формы, называемые палеттами. Зубчатое ходовое колесо нахо­дится под воздействием цепочки с гирей или закручен­ной пружины, которые стремятся повернуть его по часовой стрелке. Однако большую часть времени колесо упирается одним из зубьев в боковую поверхность той либо иной палетты, скользящей при кача­нии маятника по поверхности зуба. Только в моменты, ког­да маятник находится вблизи среднего положения, палетты перестают преграждать путь зубьям и ходовое колесо про­ворачивается, толкая анкер зубом, скользящим своей вер­шиной по скошенному торцу палетты. За полный цикл качаний маятника (за период) ходовое колесо проворачивается на два зуба, причем каж­дая из палетт получает по толчку.

Посредством этих толчков за счет энергии поднятой гири или закрученной пружины и восполняется убыль энергии маятника, возникающая вследствие трения.

Дата добавления: 2014-01-04