Колебания в каждой точке среды — процесс периоди­ческий во времени

Процесс распространения колебаний в сплошной среде, периоди­ческий во времени и в пространстве, называется волновым процессом.

Расстояние между двумя частицами среды, испытывающими в один и тот же момент времени одинаковое смещение, называется длиной волны λ. Как мы видели выше, длина волны равна расстоя­нию, которое проходит волна за один период:

λ=сТ. (5)

Равенство (3) можно записать в виде

(6)

Частицы среды колеблются с одинаковой амплитудой, но точка, отстоящая на x₁ от начальной, имеет относительно нее сдвиг фаз . На расстоянии одной длины волны фаза колебания изменяется на 2π. Величину 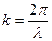— называют волновым числом. Оно показывает, сколько длин волн укладывается на отрезке длиной 2π. Вводя вол­новое число, уравнение бегущей волны можно записать в виде

(7)

Уравнения (2), (3), (4) и (5) совершенно равноправ­ны. Они описывают один и тот же волновой процесс.

Как и в случае распространения импульса, частицы среды не перемещаются вслед за волной. При прохождении волны они лишь колеблются около положения равновесия. Еще в XV в. Леонардо да Винчи, гений, соединявший в себе наблюдательность художника и интуицию ученого, писал: «Волнения гораздо подвижнее воды, поэтому часто случается так, что волна ускользает от места ее возникновения, а вода остается на том же месте, подобным же обра­зом ведут себя волны, создаваемые ветром на некошеном поле: волны бегут по полю, а стебли злака остаются на месте».

Скорость распространения волны с — это скорость распростра­нения возмущения, вызывающего смещение частиц от положения равновесия. Если на поверхность озера положить в направлении распространения волн веревку с пробковыми поплавками, отстоя­щими друг от друга на равных расстояниях, то легко заметить, что поплавки и веревка в целом не перемещаются в направлении движе­ния волны. Они лишь поднимаются и опускаются, причем в из­вестной и постоянной последовательности.

Мы видели, что точки, отстоящие друг от друга на расстоянии, равном длине волны λ =сТ, колеблются в одинаковой фазе. Можно сказать, что фаза за время одного периода «пробегает» расстояние λ или движется со скоростью с. Поэтому скорость распространения волны называют фазовой скоростью. Если в данной среде скорость распространения импульса не зависит от его величины и формы, фазовая скорость совпадает со скоростью распространения отдель­ного импульса.

Как следует из уравнения (5),

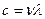. (8)

За время одного полного колебания фиксированной частицы сре­ды (4) волна (2) распространяется на расстояние, равное длине волны. Если частица в секунду совершает ν колебаний, то волна проходит ν длин волн.

Если смещения частиц среды от положения равновесия в волне параллельны направлению ее распространения, волна называется продольной, если перпендикулярны — поперечной

Дата добавления: 2014-01-04