Кинетическая и потенциальная энергия стоячей волны

Выделим в среде, где установилась продольная стоячая волна, элементарный объем ΔV, достаточно малый, чтобы можно было считать скорости колебательного движения частиц одинако­выми, а деформацию однородной. Выделенный объем обладает кинетической энергией

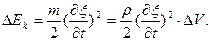
Так как для стоячей волны

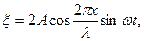то

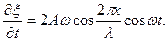
Подставив это выражение в формулу для ΔЕ_к, получаем:

. (3)

Отсюда видно, что кинетическая энергия, выделенного объема изменяется во времени, как квадрат косинуса, и что существуют такие точки волны, в которых кинетическая энергия равна нулю в любой момент времени (). Эти точки называются узлами кинетической энергии. Они совпадают с узлами смеще­ния. Точки, в которых ΔЕ_к имеет наибольшее значение (), называются пучностями кинетической энергии. Такие точки совпадают с пучностями смещения.

Выделенный объем среды ΔV обладает и запасом потенци­альной энергии

Подставляя сюда выражение

и учитывая, что , получаем:

Так как , a окончательно

(4)

Из этого соотношения видно, что потенциальная энергия фиксированного объема также изменяется во времени, но уже по закону синуса в квадрате. В те моменты времени, когда ки­нетическая энергия равна нулю (cos ωt= 0), потенциальная энергия достигает максимума (sin ωt= 1). Это значит, что ко­лебания кинетической и потенциальной энергии сдвинуты во времени на четверть периода (T/4). Напомним, что в бегущей волне оба вида энергии изменяются в одной фазе.

Потенциальная энергия зависит не только от времени, но и от положения выделенного объема ΔV. Имеются такие точки стоячей волны, где потенциальная энергия равна нулю в любой

момент времени (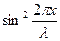). Эти точки называются узлами потенциальной энергии. Существуют и пучности потенциальной энергии (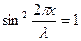).Сопоставляя (3) с (4), приходим к выводу, что узлы потенциальной энергии приходятся на пучности кинетической энергии. И наоборот, пучности потен­циальной энергии совпадают с узлами кинетической энергии. На рисунке 7 показаны графики распределения амплитуд кинетической энергии и потенциальной энергии.

Рис.7

Из графиков видно, что пучности кинетической энергии и пучности потенциальной энергии сдвинуты в пространстве на четверть длины волны (λ/4). Таким образом, в отличие от бегущих волн максимумы ки­нетической и потенциальной энергии разобщены не только во времени на (на T/4), но и в пространстве (на λ/4).

Когда кинетическая энергия волны максимальна, ее потен­циальная энергия равна нулю. Через четверть периода кинети­ческая энергия обращается в нуль, потенциальная энергия до­стигает максимума. Однако участки среды, где наблюдаются максимумы потенциальной энергии, отстоят на λ/4 от тех участ­ков, где четверть периода назад была максимальна кинетиче­ская энергия. В стоячей волне наблюдается периодически по­вторяющийся переход кинетической энергии в потенциальную и обратно, что в определенной степени аналогично переходам энергии в простой колебательной системе (например, математи­ческом маятнике). В отличие от бегущих стоячие волны не переносят энергии. Действительно, кинетическая энергия через Т/4 перейдет в потенциальную и переместится в пространстве на четверть волны, например в сторону положительных х. В сле­дующую же четверть периода потенциальная энергия вновь перейдет в кинетическую и переместится и пространстве на λ/4 в противоположную сторону.

Таким образом, средний за каждый полупериод поток энер­гии через площадку, поставленную перпендикулярно оси х, бу­дет равен нулю.

Дата добавления: 2014-01-04