Стоячие волны

ИНТЕРФЕРЕНЦИЯ ВОЛН

Явление интерференции состоит в таком наложении двух (и более) волн, которое приводит к стационарному (не завися­щему от времени) усилению колебаний частиц среды в одних местах и ослаблению (или полному погашению) в других ме­стах пространства. Если в некоторой упругой среде распростра­няются две волны, то каждая частица среды, через

которую проходят обе волны, будет одновременно участвовать в двух независимых колебательных движениях, вызванных каждой вол­ной. Результирующее движение частицы зависит от частот, ам­плитуд и начальных фаз составляющих колебаний. Однако если распространяющиеся волны имеют одинаковые частоты и если они в данной точке пространства вызывают колебания частицы вдоль одной и той же прямой, то возникает либо усиление ко­лебаний, либо их ослабление (погашение), в зависимости от разности фаз составляющих колебаний.

В пространстве всегда найдутся такие точки, в которых раз­ность фаз пришедших колебаний составит 2kπ (где k — целое число). Следовательно, в этих точках будет устойчивое (неиз­менно продолжающееся все время) усиление колебаний частиц среды. Найдутся и такие точки, в которых разность фаз при­шедших колебаний будет равна (2k +1)π. В таких точках про­странства будет наблюдаться устойчивое ослабление колебаний частиц среды. В результате область пространства, в которой волны накладываются одна на другую, будет представлять со­бой чередование участков с усиленным колебанием частиц среды и участков, где колебания частиц ослаблены или частицы вовсе не колеблются.

Понятно, что интерференционная картина возникает только при наложении таких волн, которые имеют одинаковую ча­стоту, постоянную во времени разность фаз в каждой точке про­странства и создают в каждой точке пространства колебания вдоль одной прямой. Волны, удовлетворяющие этим трем ус­ловиям (и источники, их создающие), называют когерентными.

Простейший случай интерференции наблюдается при нало­жении бегущей и отраженной волн. Эти волны когерентны (для них выполняются все три условия когерентности). Наложение таких волн приводит к образованию так называемой стоячей волны.

Смещение в стоячей волне. Запишем уравнения двух плоских волн, имеющих одинаковые частоты и амплитуды и распростра­няющихся в противоположных направлениях:

.

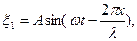
Суммарное смещение частицы среды с координатой х равно сумме смещений ξ₁ и ξ₂

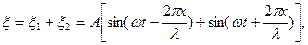
или (после тригонометрических преобразований):

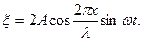(1)

Это и есть уравнение стоячей волны. Оно показывает, что в ре­зультате наложения прямой и обратной волн точки среды ко­леблются так, что все они одновременно проходят положение равновесия (sin ω t = 0) и все они одновременно достигают своих наибольших отклонений (sin ω t = ± 1).

Можно было бы сказать, что частицы в стоячей волне ко­леблются в одной фазе. Однако в силу того, что множитель 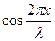имеет алгебраический знак, частицы на самом деле

колеблются либо в одной фазе, если для них 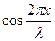имеет одинаковый знак, либо в противофазе, если 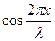имеет для них разные знаки.

Рис.4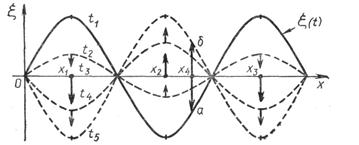

Для пояснения сказанного на рисунке 4 приведено распределение смещения частиц среды для различ­ных последовательных моментов времени. В моменты вре­мени t₁ и t₅ частицы имеют наибольшие отклонения (если иметь в виду поперечную волну в шнуре, то графики описывают ис­тинное положение частиц в пространстве), при этом скорости их равны нулю. В момент t₃ частицы проходят положение рав­новесия; скорости их максимальны. Для моментов t₂ и t₄ по­казаны распределения смещений между наибольшим и нулевым смещением. На графике выбраны три точки с координатами х₁, x₂, x₃. Для каждого момента времени стрелками показаны скорости этих точек. Из графика видно, что точки х₁ и х₂ колеблются в противофазе, а точки х₁ и x₃ — в одной фазе. Размахи колебаний у разных точек различны. Так, точка 4 колеб­лется в пределах отрезка а, б. Амплитуда колебаний частиц в стоячей волне зависит от их координаты, но не зависит от времени:

. (2)

Здесь знак модуля поставлен потому, что амплитуда — сугубо положительная величина. В стоячей волне имеются такие точки, которые остаются все время неподвижными. Такие характерные точки называются узлами смещения. Положение их определяется из условия

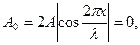
или

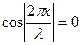
Это уравнение удовлетворяется при значениях аргумента

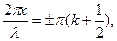
где k = 0, 1, 2,.... Отсюда

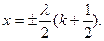
Таким образом, точки с координатами являются узлами смещения. Расстояние между двумя соседними узлами равно .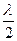

Точки волны, колеблющиеся с наибольшими амплитудами, называются пучностями смещения. Координаты этих точек оп­ределяются из условия

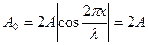
или

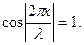
Это уравнение удовлетворяется при значениях аргумента 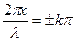(где k =0,1,2,…).

Отсюда получаем:

.

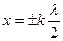Таким образом, наибольшую амплитуду имеют точки с координатами 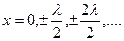Расстояние между двумя соседними пучностями равно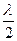. На рисунке 5 представлен график распределения амплитуды колебаний в стоячей волне (формула 2).

График стоячей волны, приведенный на рисунке 6, носит условный характер: на нем показано, в каких пределах колеб­лются различные точки среды, в которой образовалась стоячая волна. На этом графике хорошо видны узлы и пучности смеще­ния.

Рис.5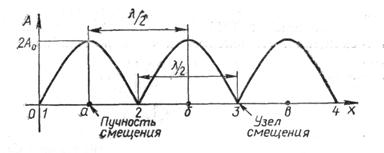

Рис.6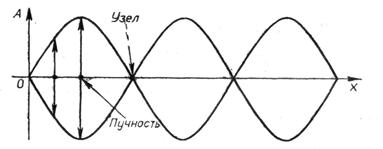

Дата добавления: 2014-01-04