Асимптотические нотации. Асимптотические обозначения

Скорость роста алгоритма. Временная сложность алгоритма

При анализе алгоритма часто будет интересовать не временное соотношение, а число операций, которые необходимые для выполнения конкретной задачи, а еще лучше – скорость роста числа операций с ростом n.

Пример: 100 входных данных, .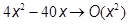

Функции имеют недостаток:

· являются достаточно волнистыми;

· требуют слишком много информации для точного представления.

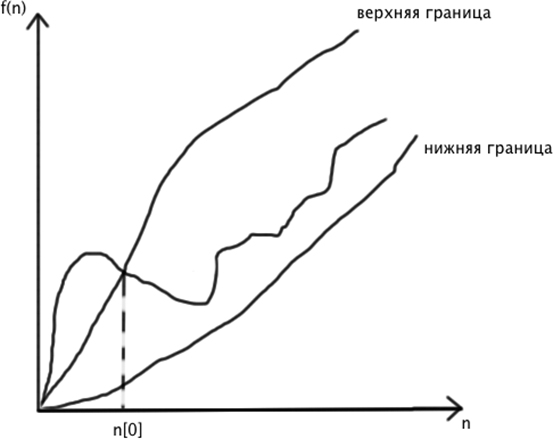
Намного легче работать с верхними и нижними границами функций временной сложности, используя для этого обозначения O-большое для верхней границе и 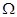-большое для нижней границы. Асимптотические обозначения позволяют упростить анализ, так как игнорируют детали, которые не влияют на сравнение эффективности алгоритмов. В частности, в асимптотических обозначениях не учитываются постоянные коэффициенты не принимаются во внимание.

Пример: .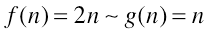

Функция 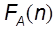, определенная как наибольшее количество элементарных действий при решении задачи размером n с помощью алгоритма A называется сложностью (временной сложностью алгоритма).

Сложность алгоритма решения почти всех реальных задач является неубывающей функцией. Аналитическое получение такой функции – достаточно сложный процесс и не нужно. Практическое значение имеет порядок возврастания 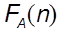с ростом n. Порядок задается с помощью другой функции, которая имеет простое аналитическое выражение и является приближенной оценкой .

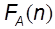Функция 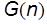называется оценкой сверху, если существует положительное число C и некоторое пороговое 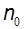, для которых 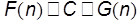при 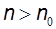. Обозначается: .

Функция 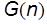называется оценкой снизу, если существует положительное число C и некоторое пороговое 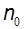, для которых 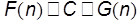при .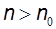

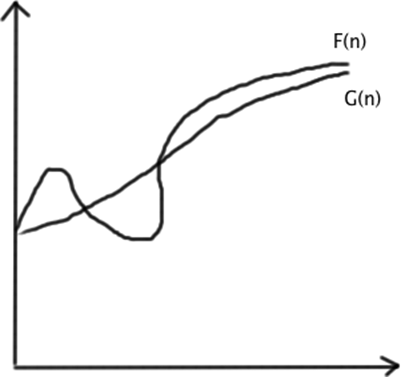
Функция 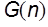называется оценкой 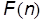, если существуют положительные конечные константы 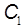и 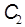, для которых 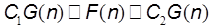. Обозначается:

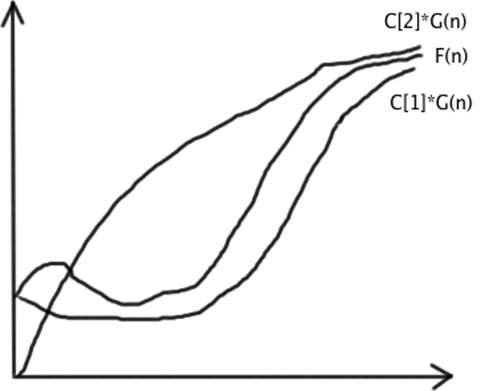
Если , то 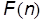является асимптотически точной оценкой для .

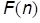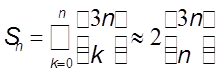при .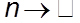

Говорят, что сумма имеет асимптотику .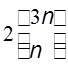

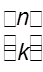- число способов выбора k-элементного подмножества из n-элементного множества.

Слово «асимптотика» имеет греческое происхождение и буквально означает «никогда не соединяющийся».

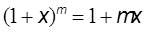
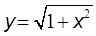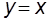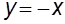: асимптоты и при .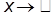

Скорость роста основных функций, определяющих оценку F(n)

Каждая операция выполняется за 1 нс.

n/f(n)	lg(n)	n	n*lg(n)	n^2	2^n	n!
	0.003 мкс	0.01 мкс	0.033 мкс	0.1 мкс	1 мкс	3.63 мкс
	0.004 мкс	0.02 мкс	0.086 мкс	0.4 мкс	1 мс	77.1 лет
	0.005 мкс	0.03 мкс	0.147 мкс	0.9 мкс	1 с	8.4 * 10^15 лет
	0.006 мкс	0.05 мкс	0.282 мкс	2.5 мкс	13 дней

1. Функция-константа: сравнение, присваивание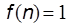

2. Логарифмическая функция:

3. Линейная функция: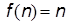

4. Суперлинейная: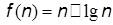

5. Квадратичная функция:

6. Кубическая функций: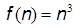

7. Показательная функция: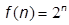

8. Факториальная функция: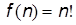

· Логарифмическая временная сложность проявляется в таких алгоритмах, как двоичный поиск, с ростом n такая функция растет очень медленно.

· Линейная: такие функции измеряют трудоемкость просмотра каждого элемента в массиве.

· Суперлинейная: важный класс функций, возникает в таких алгоритмах, как quicksort (Хоара), mergesort (сортировка слиянием).

· Квадратичная: возникает в прямый методах сортировки: пузырек, выбор, вставки.

· Кубическая: возникает при перечислении всех триад элементов в универсальном множестве из n элементов. Такая же оценка идет в динамическом программировании.

· Показательная: возникает при перечислении всех подмножеств множества из n элементов.

· Факториальная: определяет все перестановки n элементов.

Отношения доминирования функций:

Дата добавления: 2014-01-04