Доходность

Subsections

Основные измерители финансовых рынков

В основе теории финансовых рынков лежат два основных принципа, отлаженных более чем 5-ю веками банковской ¹деятельности:

Сегодняшний рубль (доллар, йена, марка, манат,...) ценнее завтрашнего,

Предполагаемый рубль (доллар, йена, марка, манат,...) дешевле гарантированного.

Первый из этих принципов находит свое отражение в операциях вычисления доходностей и дисконтирования.

• Доходность
• Дисконтирование и приведенная стоимость
• Риск в финансовых моделях

Отношение завтрашнего дохода, который можно извлечь из определенного капитала, к его сегодняшней стоимости определяет ставку дохода (rate of return):

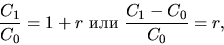
(1)

где 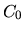-- сегодняшняя номинальная стоимость, 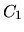-- завтрашняя номинальная стоимость какого-либо актива, 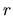-- ставка дохода.

Вычисления (1) относятся к определенному интервалу времени, ''завтра'' традиционно означает в финансовых расчетах год, а 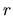-- годовую ставку дохода. Доходность типично измеряется в процентах годового прироста, т.е. 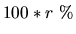. Таким образом 5% годовых означают .

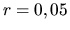В различных кредитных операциях обычно оговаривают доходность, которая, однако, может вычисляться по различным правилам.

В краткосрочных сделках используется, как правило, формула простых процентов, аналогичная (1): 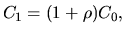где 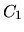-- возвращаемая сумма, 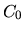-- занимаемая, а 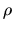-- процент по кредиту или, что равносильно, доходность для кредитующей организации ². Если сделка заключается на срок до года, 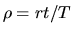, где 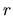-- ''годовая'' ставка доходности, 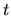-- срок в днях, на который выдается кредит, а 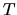-- продолжительность банковского года. То и другое может отличаться от астрономического или солнечного времени: чтобы не усложнять себе жизнь, банкиры часто считают, что в месяце 30 дней, а в году -- 360.

В долгосрочных сделках, а также при аналитических расчетах чаще используется формула сложных процентов:

(2)

где 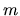-- число периодов, к каждому из которых относят доходность 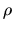. Эта формула особенно важна при анализе финансовых потоков, поступающих в финансовый инстутут и реинвестируемых в другие проекты, или используемых для выдачи иных кредитов. При 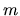-кратном использовании первоначального капитала с накапливающимися при каждой операции простыми процентами, итоговый доход будет равен (2). ³

В реальных расчетах применяются и комбинированные схемы, когда, скажем, за целое число лет вычисляют сложные проценты, а за неполный год расчет производят по формулам простых процентов. При этом формула для вычисления ставки доходности принимает вид:

(3)

где 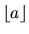-- наибольшее целое число, не превосходящее , 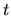-- момент времени (в днях, от некоторого начального момента), на который расчитывается доходность, 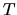-- продолжительность года (в днях), 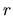-- годовая ставка доходности. Формула (3) дает завышенные результаты по сравнению с ''простой'' формулой сложных процентов . Разница ⁴ в доходности представлена на рис. 1.2.1.

Figure: Разность доходностей между коминированной схемой начисдения процентов и формулой сложных процентов при нормативной годовой доходности 20%. По оси абсцисс отложены дни, по оси ординат -- разность доходностей в процентах.

Подробное обсуждение различных схем вычисления доходностей можно найти, например, в [6].

Вводя в формулу (1) явным образом время, ее можно переписать как

или, переходя к пределу по ,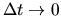

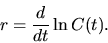
(4)

Выражение справа определяет для капитала так называемую ''мгновенную'' доходность (force of interest), часто использумую как некоторый первичный фактор в финансовых моделях с непрерывным временем.

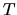Считая левую часть уравнения (4) заданной как некоторую функцию времени и интегрируя его от до некоторого , получаем

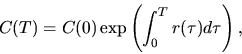
что дает при постоянной ''мгновенной'' доходности 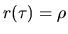выражение для средней доходности за период :

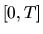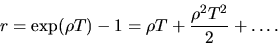
(5)

При малых 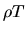это соотношение дает результаты, близкие к формуле простых процентов. С другой стороны, полагая в (5) 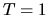(один год) получаем обратное соотношение для эквивалентной мгновенной доходности .

Дата добавления: 2014-01-04