Дисконтирование и приведенная стоимость

Родственную или, скорее говоря, обратную к доходности величину

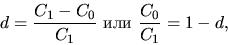
где 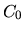-- сегодняшняя номинальная стоимость, 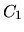-- завтрашняя номинальная стоимость какого-либо актива, называют коэффициентом дисконтирования или просто дисконтом. Очевидно 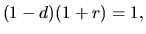где 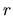-- доходность капитала, определенная выше. Дисконтирование будущих доходов или, иначе говоря, вычисление их текущей стоимости (present value, PV) -- это одна из основных ⁵операций в финансовой математике.

Приведенная стоимость будущих доходов 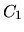определяется как дисконтированые будущие доходы:

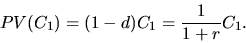
Содержательно она обозначает ту минимальную сумму денег, которую нужно положить в банк под проценты 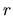с тем, чтобы получить в конце года 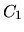рублей. Тем самым операция открытия банковского счета на сумму 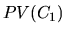и та подразумеваемая экономическая деятельность, которая связана с получением будущего дохода 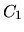становятся с точки зрения инвестора эквивалентными. Наличие таких эквивалентных схем черезвычайно важно для математической теории финансовых рынков и часто так или иначе закладывается в исходные предпосылки различных теорий. Упрощая, можно сказать, что в равновесном рынке все возможности вложения капитала должны быть с точки зрения инвестора эквивалентыми.

Свое первое применение 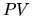находит в оценках экономической целесообразности инвестиционных проектов. Проект, требующий инвестиций в обьеме 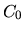и обещающий будущий доход 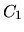, экономически целесообразен для инвестора только в том случае, если

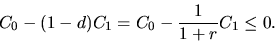
Здесь 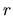может быть доходностью альтернативных вложений капитала, сравнимых с данным проектом по остальным параметрам (обьемам инвестиций, уровню риска и пр.). Считая 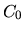отрицательным, поскольу это расходы инвестора, последнее неравенство можно переписать в виде

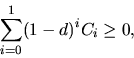
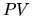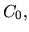
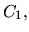
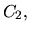
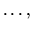
что подсказывает обобщение принципа неотрицательности на случай потока платежей 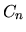в равноотстоящие моменты времени при дисконтировании 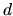на каждом интервале времени:

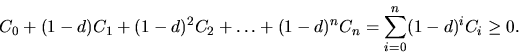
(6)

Равенство нулю можно рассматривать как некоторый крайний случай и использовать его для определения эффективного дисконта 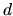или, что эквивалентно, эффективной доходности.

Уравнение (6) можно решить аналитически только для небольших 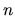. В общем случае его решают численно, с применением тех или иных приближенных методов. Любопытно отметить, что один из методов решения уравнения (6) для высоких степеней 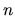принадлежит Н.И. Лобачевскому, более известному как одному из авторов неэвклидовой геометрии.

Дата добавления: 2014-01-04