Мартингалы и возможности арбитража

Отсутствие на рынке возможностей извлекать безрисковую прибыль тесно связано со свойствами случайных последовательностей стоимостей рискованных активов. Особенно важным оказывается при этом класс случайных последовательностей, называемых мартингалами.

Для того, чтобы проанализировать связи между мартингалом и арбитражем, мы должны прежде всего определить мартингал на конечном вероятностном пространстве.

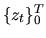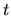Определение 6 Последовательность случайных величин адаптирована к фильтрации если для любого случайные величины 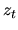измеримы относительно .

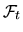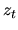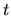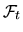Содержательно это означает, что значения определяются событиями, происшедшими до момента включительно. Через (см. Приложение) обозначим условное математическое ожидание относительно . Иногда, когда 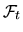сами порождаются последовательностями случайных величин 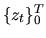такое условное мтатематическое ожидание обозначают и .

Особок значение для финансовой математики имеют следующие типы случайных последовательностей.

Определение 7 Адаптированная последовательность действительных случайных величин

• мартингал, если , для всех .
• супермартингал, если 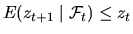для всех .
• субмартингал, если для всех .

Примером мартингала является сумма независимых случайных величин, 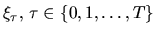, имеющих нулевые средние значения:

(27)

Фильтрацию можно определить в этом случае, как последовательность наименьших 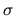-алгебр 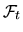, таких, что измеримы относительно 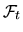. Как уже упоминалось, такие 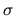-алгебры называются порожденными случайными величинами . Тогда

В силу независимости

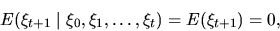
откуда следует, что .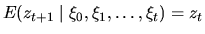

Если , то последовательность (27) является субмартингалом, а если , то супермартингалом. В определенном смысле это аналоги невозрастающих или неубывающих последовательностей.

Если последовательность случайных величин является мартингалом, то математичекое ожидание ее элементов постоянно:

Для описания процессов, происходящих на финансовых рынках, отсутствия на них предсказателей будущего, требует введения еще одного понятия.

Определение 8 Адаптивная последовательность случайных величин предсказуема, если для всех 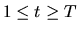величина 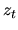измерима относительно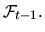

Содержательно это означает, что значения 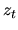определяются событиями, происшедшими до момента включительно.

Свойство случайной последовательности быть мартингалом сохраняется при некоторых преобразованиях, определяемых предсказуемыми случайными величинами.

Определение 9 Пусть -- мартингал, - предсказуемая относительно фильтрации последовательность случайных величин. Последовательность , определенная как

называется мартингальным преобразованием (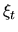по ).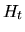

Теорема 10 Мартингальное преобразование мартингала по предсказуемой является мартингалом.

Д о к а з а т е л ь с т в о. Очевидно, - адаптированная последовательность. Более того, для

в силу 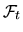-измеримости 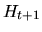(см. Приложение). Следовательно,

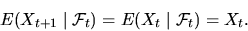
Последнее показывает, что является мартингалом.

Из этого предложения и (24) следует, что если дисконтированные цены финансовых инструментов представляют собой мартингалы, то дисконтированное значение портфеля, порождаемого СФ-стратегией, также является мартингалом. Действительно,

поэтому

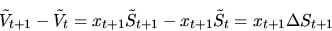
и в силу 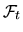-измеримости 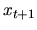является мартингальным преобразованием по .

Мартингальность легко проверить и непосредственно:

Отсюда следует, что при мартингальных дисконтированных ценах активов среднее (ожидаемое) значение приведенной стоимости портфеля, порождаемого самофинансирующейся стратегией, равно начальному капиталу.

Содержательно это означает, что в номинальном значении капитал инвестора в среднем растет так же, как и его безрисковый банковский счет. Однако следует подчеркнуть, что цены рисковых активов являются мартингалами лишь относительно весьма специальных риск-нейтральных вероятностных мер. Эти меры не имеют особого отношения к реальным вероятностям тех или иных экономических событий (если вообще в экономических ситуациях можно говорить о вероятности, против чего многие практики яростно возражают). Риск-нейтральные меры являются лишь удобным формализмом представления выражений для цен производных ценных бумаг, а их существование или несуществование указывает на отсутствие или наличие арбитражных возможностей.

Утверждение теоремы 10 можеть быть в определенном смысле и обращено, что дает некоторое характерное свойство мартингалов, которое мы далее будем использовать.

Теорема 11 Адаптированная последовательность действительных случайных величин 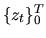является мартингалом тогда и только тогда, когда для любой предсказуемой последовательности

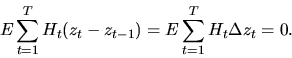
(28)

Д о к а з а т е л ь с т в о. Необходимость. Если 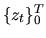- мартингал, то определив 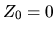и далее

получаем, что в силу теоремы 10 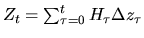является мартингалом и, следовательно,

(29)

Достаточность. Для доказательства достаточности предположим противное, т.е. пусть для некоторого 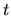существует множество элементарных событий 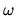таких, что 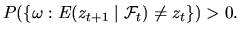Тогда либо

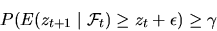
(30)

либо

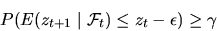
для некоторых

Пусть для определенности выполнено (30). Обозначим через соответствующее подмножество элементарных исходов:

По построению . Определим

где -- индикатор множества :

Из 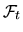-измеримости следует предсказуемость 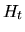. Построим с помощью 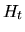соответствующую последовательность :

По построению

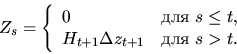
и для этой последовательности должно быть выполнено равенство (28).

Однако,

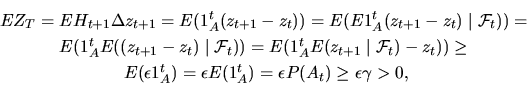
что противоречит (28) и, следовательно, доказывает теорему

Дата добавления: 2014-01-04