Совершенные рынки и цены опционов

Как мы уже упоминали ранее, одним из наиболее распространенных финансовых инструментов является опцион, зародившийся на основе торговли луковицами тюльпанов в Голландии в 17-ом веке. В своем наиболее общем виде опцион -- это оплаченное право купить или продать в будущем какой-либо актив или материальную ценность на заранее определенных условиях.

Простейший из опционов -- европейский заключается на право купить (call) некий актив в фиксируемую на момент продажи опциона дату 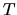. Цена , по которой будет совершена сделка, также фиксируется. Европейский опцион может быть также заключен на право продажи. В этом случае он называется put -опционом.

С формально-математической точки зрения можно определить европейский опцион со сроком исполнения 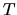, задав его функцию выплат 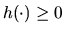. Функция выплат может зависеть от различных аргументов, для целей последующего изложения единственным условием является ее 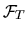-измеримость. В простейшем случае европейского call-опциона выплата зависит от стоимости финансового инструмента 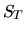в момент исполнения 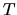и цены исполнения :

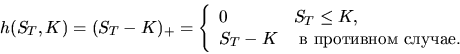
Содержательный смысл этой величины заключается в том, что продав в момент 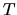финансовый инстумент по цене , лицо, выпустившее опцион дает возможность его владельцу немедленно заработать на разнице договорной цены и текущей рыночной стоимости инструмента 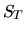(конечно, если 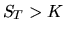). Если же 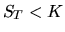, владельцу опциона не имеет смысла его реализовать.

Европейский опцион на продажу того же инструмента будет определен как

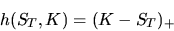
и интерпретируется таким же образом: если 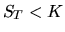, владелец опциона может немедленно заработать 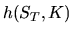на разнице договорной цены и текущей рыночной стоимости инструмента 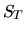, купив на рынке актив по цене 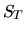и продав его эмитенту опциона по цене . Если же 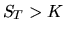, владельцу опциона не имеет смысла его реализовать.

Поскольку опцион -- это оплаченное право, его покупатель в любом случае выплачивает эмитенту некоторую стоимость опциона и одним из основных вопросов теории вторичных или производных ценных бумаг и опционов в частности, является определение их так называемой справедливой цены. Такая цена должна исключать арбитражные возможности и отражать конкурентно-равновесное состояние рынка.

В первую очередь условия отсутствия арбитражных возможностей приводят к весьма специальным соотношениям между ценами финансовых инструментов, в частности между ценами put и call опционов. Соотношение между ними носит название call-put эквивалентности.

Для вывода этого соотношения представим портфель, состоящий из 4-х видов финансовых инструментов: рискового актива (акции), европейских call и put опционов на эту акцию с одним и тем же сроком исполнения 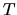и договорной ценой исполнения и банковского счета (безрискового актива) с доходностью 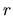. Пусть структура портфеля (количество данного актива в портфеле) задается первой строкой табл. 3.4.

Table: Структура цен портфеля опционов.
	акция	put-опцион	call-опцион	банковский счет
Структура портфеля			-1	Z
Стоимости в
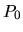
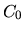
Стоимости в

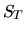
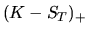
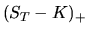
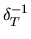
Заметим, что call-опцион содержится в портфеле в отрицательном количестве, что соответствует короткой позиции (заем).

Пусть цены call-put опционов подобраны так, что начальная стоимость портфеля равно нулю:

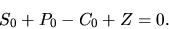
(31)

Стоимость активов в момент исполнения опционов приведена в третьей строке таблицы, где 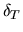, как обычно, коэффициент дисконтирования 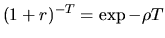. Соответственно стоимость портфеля в момент исполнения опционов равна

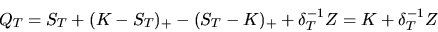
и не зависит от стоимости рискованного актива.

Условие отсутствия арбитража в этом случае сводится к равенству 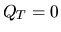: если 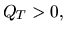то имеет место чисто арбитражная ситуация -- безрисковая положительная прибыль при нулевом начальном капитале. При 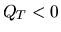достаточно изменить знаки позиций активов на противоположные и снова получить безрисковую положительную прибыль. Уравнение

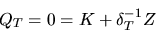
определяет , что при подстановке в (33) и дает соотношение call-put эквивалентности

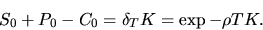
(32)

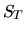В этих двух примерах опционов выплата зависела только от . Существуют опционы, зависящие от всей предыстории финансового инструмента, т.е. в этом случае является функцией всей последовательности 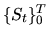или ее части. Это, например, так называемый азиатский опцион, когда цена исполнения равна средней цене инструмента, наблюдаемой в течение определенного времени перед исполнением, или парижский, где выплата зависит от того, превышает ли рыночная стоимость актива некоторый уровень на протяжении определенного интервала времени перед исполнением опциона.

В дальнейшем нам потребуется использовать понятие заявки (claim, contingent claim). Это понятие представляет собой предложение купли или продажи, высталенное на рынок, но еще не нашедшее встречного предложения. Условия заявки в контексте опциона сводятся к определению его срока действия и функции выплат.

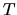Определение 12 Заявка, определяемая , называется достижимой, если существует допустимая стратегия , имеющая в момент стоимость 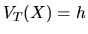для всех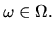

Фундаментальное значение имеет тот факт, что для обеспечения выполнения условий опциона необходимо всего лишь найти на финансовом рынке самофинансирующуюся стратегию, которая имеет в момент исполнения стоимость и знать вероятностную меру, относительно которой дисконтированные цены являются мартигалами.

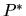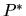В самом деле, если -- это СФ-стратегия и -- вероятностная мера, эквивалентная , такая, что дисконтированные цены являются мартингалами относительно этой меры, то также является -мартингалом, будучи мартингальным преобразованием 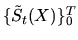. Следовательно, для

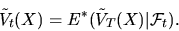
(33)

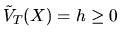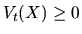Выберем так, чтобы в конечный момент времени . Тогда, согласно (35) и, следовательно, , т.е. стратегия -- допустима. Поскольку в конечный момент времени значение портфеля совпадает с функцией выплат, то, продав этот портфель, эмитент может рассчитаться с покупателем опциона.

Определение 13 Рынок называется совершенным (complete), если каждая заявка достижима.

Предположение о том, что финансовый рынок является совершенным, достаточно ограничительно и не имеет такого ясного экономического обоснования, такого как, например, предположение об отсутствии арбитражных возможностей. Вместе с тем привлекательная особенность совершенных рынков заключается в том, что для таких рынков можно построить простую теорию цен заявок и хеджирования.

Следующая теорема дает еще одну характеризацию совершенных финансовых рынков.

Теорема 14 Рынок совершенен и нормален тогда и только тогда, когда существует единственная вероятностная мера 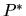, эквивалентная , относительно которой дисконтированные цены являются мартингалами.

Д о к а з а т е л ь с т в о. Необходимость. Пусть рынок нормален и совершенен. Тогда любая неотрицательная 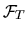-измеримая случайная величина может быть записана как 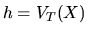, где 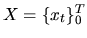-- допустимая стратегия, которая воспроизводит заявку . Поскольку -- СФ-стратегия, то

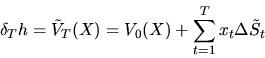
и в силу нормальности рынка существует (теорема 14) по крайней мере одна вероятностная мера, мартингализирующая 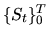. Есл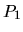и и 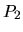-- две вероятностные меры, относительно которых дисконтированные цены являются мартингалами, то является мартингалом относительно как 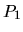так и .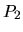

Обозначим через 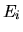математическое ожидание относительно меры 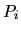, 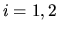. Тогда

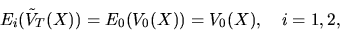
последнее равенство следует из того, что 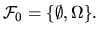Поэтому

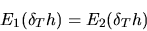
для произвольной и, следовательно, .

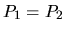Достаточность. При существовании мартингализирующей меры 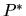нормальность рынка утверждается теоремой 14. Предположим теперь, что рынок нормален, но несовершенен. Тогда существует случайная величина (выплата) 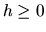, которая не реализуема.

Обозначим через множество случайных величин вида

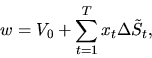
(34)

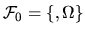где случайная величина измерима относительно и 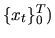-- предсказуемый процесс со значениями в 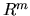. Легко видеть, что -- линейное подпространство пространства случайных величин на 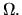Так как случайная величина 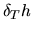не принадлежит то является строгим подмножеством множества всех случайных величин на .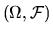

На множестве всех случайных величин на 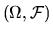можно определить скалярное произведение где 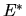-- математичекое ожидание относительно вероятностной меры 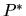, эквивалентной и относительно которой дисконтированные цены являются мартингалами. Заметим, что в силу теоремы 10

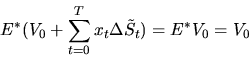
и, следовательно, .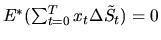

Так как не совпадает с пространством всех случайных величин на 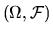, то существует ненулевая случайная величина 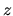, ортогональная к : 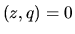для любого Определим

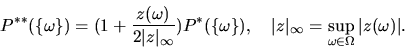
(35)

Легко видеть, чт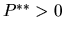о , но 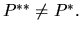Для того, чтобы убедиться в том, что 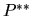-- вероятностная мера, положим в (36)

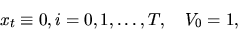
то есть 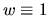. Тогда

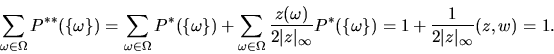
Таким образом, (37) определяет новую вероятностную меру, эквивалентную 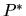, но не совпадающую с ней.

Обозначим через 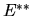математическое ожидание по мере 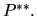Поскольку

то

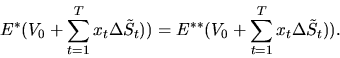
Следовательно,

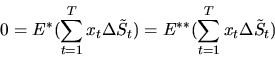
для любого предсказуемого процесса 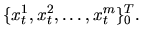Из леммы 11 следует, что 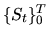является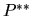-мартингалом, что противоречит предполагаемой единственности мартингализирующей меры.

Дата добавления: 2014-01-04