
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Простейшее обобщение биномиальной модели: случай трех возможных состояний
|
|
|
|
Предположим, что на каждых торгах цена акции может изменяться только в 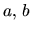 и
и 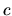 раз (
раз (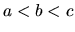 ), и решим задачу о цене опциона
), и решим задачу о цене опциона 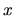 в случае
в случае 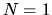 . Соответствующая задача ЛП имеет вид
. Соответствующая задача ЛП имеет вид

| (48) |
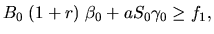
| |||
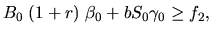
| (49) | ||

|
Здесь 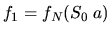 и т.д. -- значения функции выплаты при соответствующих ценовых ситуациях.
и т.д. -- значения функции выплаты при соответствующих ценовых ситуациях.
Для ее решения перейдем к двойственной задаче, которая выглядит следующим образом:
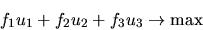
| (50) |
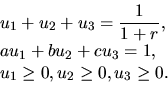
| (51) |
В дальнейшем будем использовать симплекс-метод. Чтобы определить начальный допустимый базис, воспользуемся ''методом искусственного базиса'' (см. например, [11]). Введем вспомогательные (так называемые,,искусственные") переменные следующим образом:
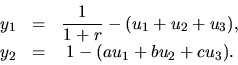
| (52) |
Для системы (54) переменные  и
и 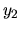 образуют допустимый базис. Если перевести эти переменные в небазисные, то они примут нулевые значения, и мы получим допустимый базис для системы (53). Для такого перевода можно использовать симплекс-метод. А именно, решим задачу минимизации функции
образуют допустимый базис. Если перевести эти переменные в небазисные, то они примут нулевые значения, и мы получим допустимый базис для системы (53). Для такого перевода можно использовать симплекс-метод. А именно, решим задачу минимизации функции  при ограничениях (54) и
при ограничениях (54) и
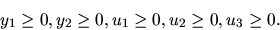
Указанная процедура приводит к следующему результату:
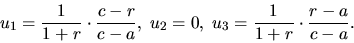
| (53) |
Взяв этот допустимый базис в качестве исходного и применяя симплекс-метод, легко видеть, что функция (50) достигает минимума, равного
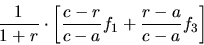
если величина

неотрицательна. Интересно отметить, что это всегда так для call-опциона с функцией выплаты 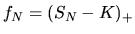 , как показывает несложный анализ. Для этого надо рассмотреть варианты соотношения величины
, как показывает несложный анализ. Для этого надо рассмотреть варианты соотношения величины  и стомости акции в момент времени
и стомости акции в момент времени 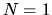 , (например,
, (например,  , и т.д.), и произвести простые алгебраические манипуляции.
, и т.д.), и произвести простые алгебраические манипуляции.
Видно, что в этом случае добавление третьего состояния не дает ничего существенно нового для определения рациональной стоимости опциона: такой же результат дает биномиальная модель по формуле (49), если вообще не рассматривать возможность изменения цены акции в 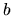 раз. На цену влияют лишь максимальный и минимальный коэффициенты.
раз. На цену влияют лишь максимальный и минимальный коэффициенты.
Однако для других функций выплаты 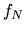 возможны и другие варианты: если
возможны и другие варианты: если 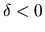 , то стоимость опциона будет
, то стоимость опциона будет
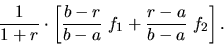
Теперь игнорируется уже состояние, соответствующее росту акций в 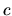 раз.
раз.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 334; Нарушение авторских прав?; Мы поможем в написании вашей работы!