
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Частица в одномерной бесконечно глубокой яме
|
|
|
|
15. Частица в одномерной бесконечно глубокой яме
Рассмотрим поведение частицы в одномерной прямоугольной потенциальной яме ширины a с бесконечно высокими стенками. В интервале от 0 до а будем считать,что потенции.энергия=0,а вне этого интервала потенциальная энергия бесконечна.
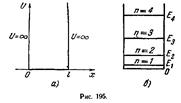 (1)
(1)
Задача состоит в том,чтобы найти те,значения энегрии, которыми обладает частица,находящаяся в яме. Чтобы найти энергию частицы необходимо решить стационарное уравнение Шредингера
Ĥψ(x)=Eψ(x) (2); (Ť+Ŭ)ψ=Eψ (3); → Ťψ=Eψ (4) -(ℏ2/2m)*(d2ψ/dx2)=Eψ (5) Поскольку U вне интервала от 0 до а равна бесконечности, то частица, находящаяся в яме проникнуть сквозь стенки не может, т.е. функция вне интервала от 0 до а равна 0. Поскольку ф-ия явл-ся непрерывной, то в точках х=0 и х=а она должна обращаться в 0: ψ(0)=ψ(а)=0 (6)
Из соотношений 5 и 6 видно,что с матем.точки зрения наша задача состоит в решении дифференц.ур-ия второго порядка с заданными граничными условиями:
(5)↔ -(d2ψ/dx2)=(2Em/ℏ2)ψ (d2ψ/dx2)+k2ψ=0 (7)
Можно показать,что решение ур-ия 7 имеет сле.вид: ψ=Asin(kx)+Bcos(kx) (8), А и В-константы, которые находятся из граничных условий и условия нормировки.
Из 6 следует,что ψ(0)=0 (9); Подставляя (8) в (9),получим: ψ(0)= Asin(0)+Bcos(0)=В=0 (10)
(10) в (8): ψ(x)=Asin(kx) (11); Из (6) → ψ(а)=0 (12); Подставляя (11) в (12): ψ(а)=Аsin(ka)=0 Поскольку А - произвольная константа, она вообще говоря не равна 0 → sin(ka)=0 (13) ka=πn(14)→ k=(π/a)n (15). Подставляя 15 в 11, получаем: ψ(x)=Asin(πnx/a) (16).
Для того,чтобы найти константу А воспользуемся условием нормировки: ∫dxψ*ψ=1 (17)
Подставляя 16 в 17, получаем: A2∫sin2(πnx/a)dx=1, решая, получаем: A=√(2/a) (19)
Подставляя 19 в 16, получим: ψ(x)= (√(2/a))* sin(πnx/a) (20)
E2m/ℏ2=π2n2/a2 → E=π2ℏ2n2/2ma2=(ℏ2/2m)*(π2/a2)*n2 (21)
Из 21 следует,что энергия частицы, находящейся в основном(самом низшем) состоянии определяется так: E1=(ℏ2/2m)*(π2/a2) (22). Из соотношения 22 следует,что энергия частицы,нах-ся в основном состоянии не равна 0.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 528; Нарушение авторских прав?; Мы поможем в написании вашей работы!